Allergy Asthma Respir Dis.  2017 May;5(3):123-127. 10.4168/aard.2017.5.3.123.

A review of asthma and immunololgic mathematical models

• Lee J

• KMID: 2379938
• DOI: http://doi.org/10.4168/aard.2017.5.3.123

Abstract

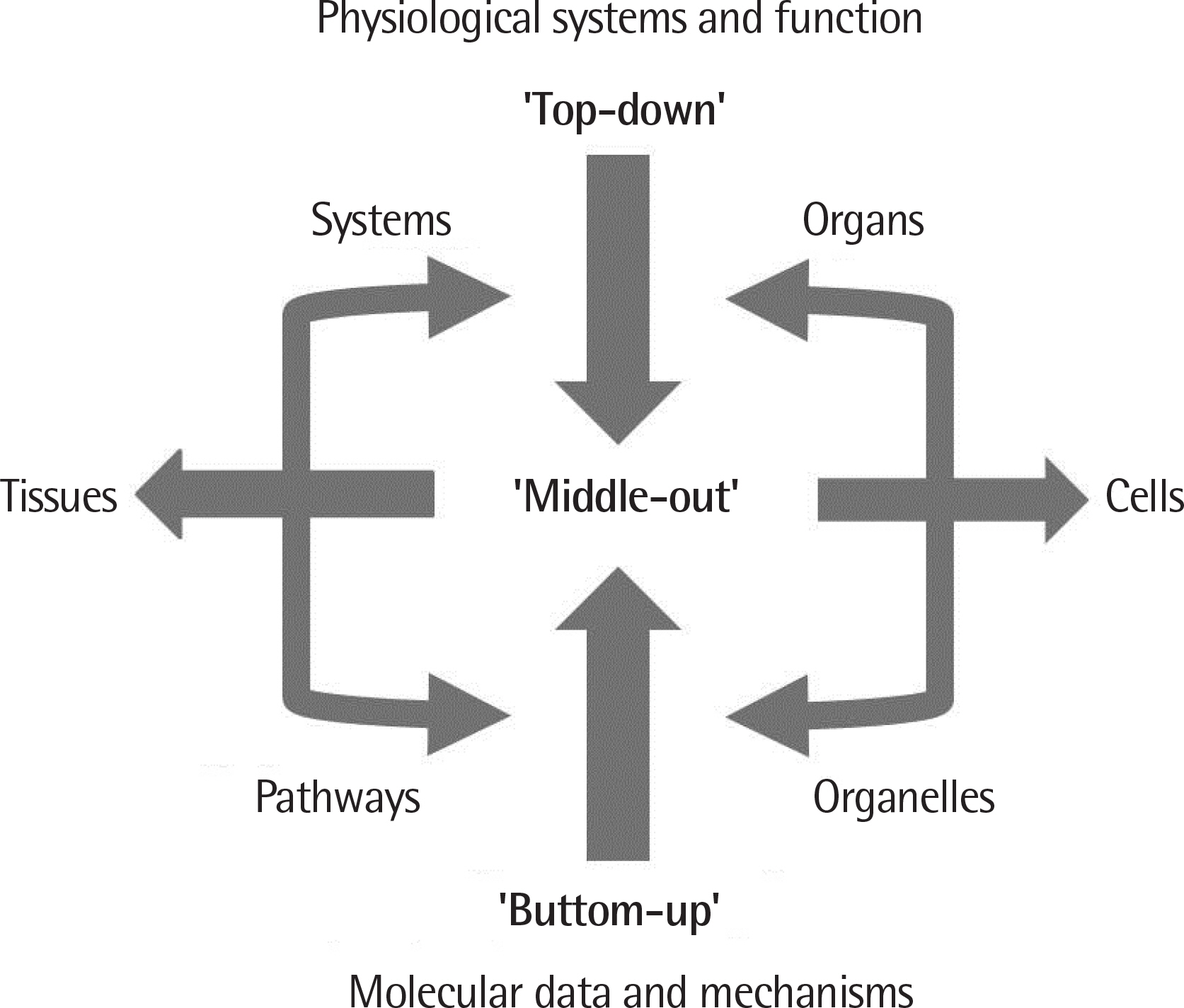
Asthma and allergic disease are of multifactorial nature like most of the other diseases that clinicians are facing. To establish the disease nature and improve the treatment success rate, it is unavoidable to examine closely enormous clinical and biological data that have been accumulated during the last century. The expanding gap between basic research and clinical medicine demand a novel approach. System biology emerged to reduce this gap as an interdisciplinary and translational method, and integrated clinical and experimental data through bioinformatics and mathematical modeling. Mathematical modeling is the method that disassembles the system, interpret the complex relations concealed among elements, and then establish a comprehensive and testable new hypothesis for the complex phenomenon or disease. To this end, we review the mathematical models dealting with asthma and immunologic system.

Keyword

Mathematical model; Simulation; Clinical trial; Asthma; Immunology

MeSH Terms

Allergy and Immunology
Asthma*
Biology
Clinical Medicine
Computational Biology
Methods
Models, Theoretical*

Figure

• 

  Fig. 1. Two main approaches in system biology. “-omics” approach proceeds first with obtaining high-throughput data produced from clinical samples and followed by statistical inference using biostatistics. A mathematical modeling proceeds first with a reconstruction of biochemical network based on published information, experimental data, and hypothesis that is relevant a given disease, then translates a mathematical model followed by using a model to prove hypotheses about the network regulation. Adapted from Sittka A, et al. Pediatr Res 2013;73:543-52.4

• 

  Fig. 2. Levels of modelling. Biological simulation can be started from either the ‘bottom’ or the ‘top.’ Alternatively, it can be started from the ‘middle,’ which starts at any level (pathways, organelles, cells, tissues, organs or systems) at which there are sufficient data and reaches (up, down, and across) towards other levels and components. Adapted from Noble D. Nat Rev Mol Cell Biol 2002;3: 459-63.1

Reference

1. Noble D. The rise of computational biology. Nat Rev Mol Cell Biol. 2002; 3:459–63.

2. Kitano H. Computational systems biology. Nature. 2002; 420:206–10.

3. Stelling J. Mathematical models in microbial systems biology. Curr Opin Microbiol. 2004; 7:513–8.

4. Sittka A, Vera J, Lai X, Schmeck BT. Asthma phenotyping, therapy, and prevention: what can we learn from systems biology? Pediatr Res. 2013; 73(4 Pt 2):543–52.

5. Höfer T, Nathansen H, Löhning M, Radbruch A, Heinrich R. GATA-3 transcriptional imprinting in Th2 lymphocytes: a mathematical model. Proc Natl Acad Sci U S A. 2002; 99:9364–8.

6. van den Ham HJ, de Boer RJ. From the two-dimensional Th1 and Th2 phenotypes to high-dimensional models for gene regulation. Int Immunol. 2008; 20:1269–77.

7. Moulton DE, Goriely A. Possible role of differential growth in airway wall remodeling in asthma. J Appl Physiol (1985). 2011; 110:1003–12.

8. Chernyavsky IL, Croisier H, Chapman LA, Kimpton LS, Hiorns JE, Brook BS, et al. The role of inflammation resolution speed in airway smooth muscle mass accumulation in asthma: insight from a theoretical model. PLoS One. 2014; 9:e90162.

9. Martonen TB, Schroeter JD, Fleming JS. 3D in silico modeling of the human respiratory system for inhaled drug delivery and imaging analysis. J Pharm Sci. 2007; 96:603–17.

10. Martonen T, Fleming J, Schroeter J, Conway J, Hwang D. In silico modeling of asthma. Adv Drug Deliv Rev. 2003; 55:829–49.

11. Martonen TB, Musante CJ, Segal RA, Schroeter JD, Hwang D, Dolovich MA, et al. Lung models: strengths and limitations. Respir Care. 2000; 45:712–36.

12. Patel B, Gauvin R, Absar S, Gupta V, Gupta N, Nahar K, et al. Computational and bioengineered lungs as alternatives to whole animal, isolated organ, and cell-based lung models. Am J Physiol Lung Cell Mol Physiol. 2012; 303:L733–47.

13. Frey U, Brodbeck T, Majumdar A, Taylor DR, Town GI, Silverman M, et al. Risk of severe asthma episodes predicted from fluctuation analysis of airway function. Nature. 2005; 438:667–70.

14. Lauzon AM, Bates JH, Donovan G, Tawhai M, Sneyd J, Sanderson MJ. A multi-scale approach to airway hyperresponsiveness: from molecule to organ. Front Physiol. 2012; 3:191.

15. Hickling KG. The pressure-volume curve is greatly modified by recruitment. A mathematical model of ARDS lungs. Am J Respir Crit Care Med. 1998; 158:194–202.

16. Gutierrez G. A mathematical model of tissue-blood carbon dioxide exchange during hypoxia. Am J Respir Crit Care Med. 2004; 169:525–33.

17. Dumesnil JG, Shoucri RM, Laurenceau JL, Turcot J. A mathematical model of the dynamic geometry of the intact left ventricle and its application to clinical data. Circulation. 1979; 59:1024–34.

18. Kohl P, Noble D, Winslow RL, Hunter PJ. Computational modelling of biological systems: tools and visions. Philos Trans R Soc A. 2000; 358:579–610.

19. Smith NP, Kassab GS. Analysis of coronary blood flow interaction with myocardial mechanics based on anatomical models. Philos Trans R Soc A. 2001; 359:1251–62.

20. Yan GX, Antzelevitch C. Cellular basis for the normal T wave and the electrocardiographic manifestations of the long-QT syndrome. Circulation. 1998; 98:1928–36.

21. DiFrancesco D, Noble D. A model of cardiac electrical activity incorpo-rating ionic pumps and concentration changes. Philos Trans R Soc Lond B Biol Sci. 1985; 307:353–98.

22. Savla U, Olson LE, Waters CM. Mathematical modeling of airway epithelial wound closure during cyclic mechanical strain. J Appl Physiol (1985). 2004; 96:566–74.

23. Castillo-Chavez C, Hethcote HW, Andreasen V, Levin SA, Liu WM. Epidemiological models with age structure, proportionate mixing, and cross-immunity. J Math Biol. 1989; 27:233–58.

24. Feng Z, Castillo-Chavez C, Capurro AF. A model for tuberculosis with exogenous reinfection. Theor Popul Biol. 2000; 57:235–47.

25. Datta M, Via LE, Chen W, Baish JW, Xu L, Barry CE 3rd, et al. Mathematical model of oxygen transport in tuberculosis granulomas. Ann Biomed Eng. 2016; 44:863–72.

26. Pienaar E, Lerm M. A mathematical model of the initial interaction between Mycobacterium tuberculosis and macrophages. J Theor Biol. 2014; 342:23–32.