Transl Clin Pharmacol.  2019 Jun;27(2):52-58. 10.12793/tcp.2019.27.2.52.

Understanding the pharmacokinetics of reversible metabolism

• Cho S
• Yoon YR

• KMID: 2457571
• DOI: http://doi.org/10.12793/tcp.2019.27.2.52

Abstract

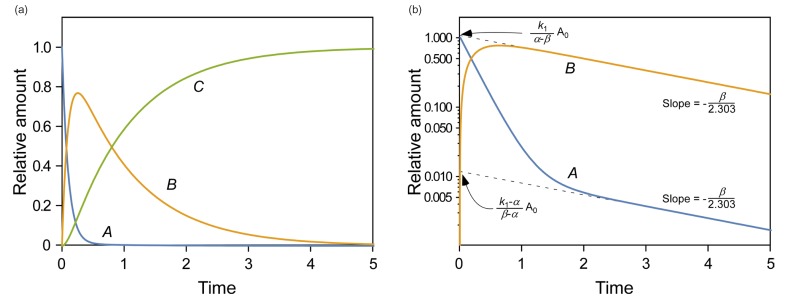
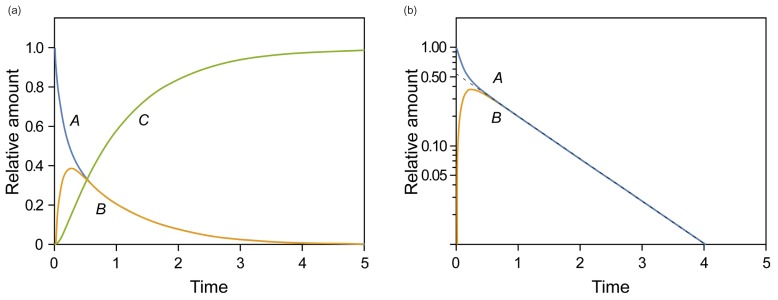
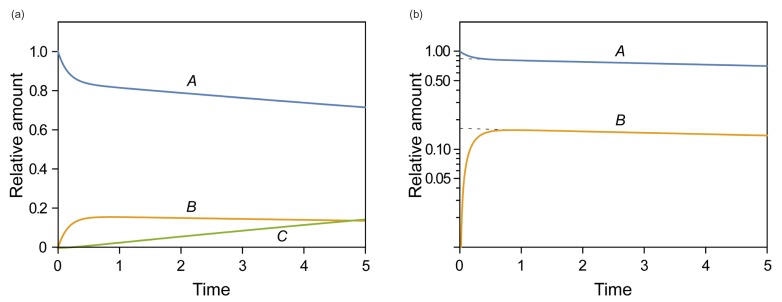
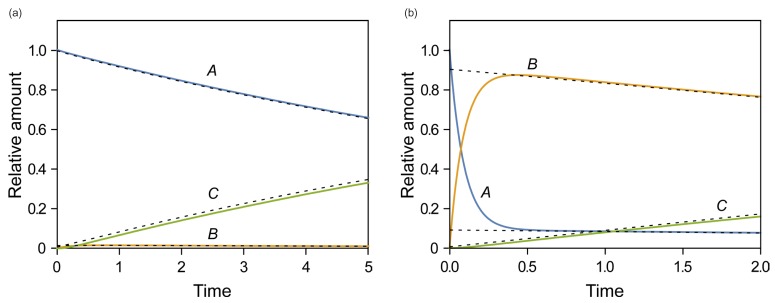
This tutorial introduces the mathematical skills required to obtain exact and approximate solutions for reversible reactions and provides graphical insights to help understand the pharmacokinetics of reversible metabolism. The matrix method provides an easy way to derive the exact solution for the amount of each species as a function of time. The plots of the exact solutions reveal some characteristic features of the pharmacokinetic profiles of the reversible metabolism. We also describe two approximation approaches, steady-state approximation, and equilibrium approximation, to simplify the solutions. The skills and knowledge acquired through this tutorial will provide a basis for understanding more complex reversible reaction systems.

Keyword

Equilibrium approximation; Matrix Method; Pharmacokinetics; Reversible Metabolism; Steady-state approximation

MeSH Terms

Metabolism*
Methods
Pharmacokinetics*

Figure

• 

  Figure 1 (a) Linear and (b) semi-logarithmic plots of the amount-time curves of A, B, or C in the reversible reaction, A k1⇄k2  B k3→ C, where k1 = 10, k2 = 0.1, and k3 = 1. The abscissa and ordinate denote the time and the amount of each species, respectively, in arbitrary unit. See text for details.

• 

  Figure 2 (a) Linear and (b) semi-logarithmic plots of the amount-time curves of A, B, or C in the reversible reaction, A k1⇄k2  B k3→ C, where k1 = 5, k2 = 4, and k3 = 2. The abscissa and ordinate denote time and the amount of each species, respectively, in arbitrary unit. See text for details.

• 

  Figure 3 (a) Linear and (b) semi-logarithmic plots of the amount-time curves of A, B, or C in the reversible reaction, A k1⇄k2  B k3→ C, where k1 = 1, k2 = 5, and k3 = 0.2. The abscissa and ordinate denote time and the amount of each species, respectively, in arbitrary unit. See text for details.

• 

  Figure 4 Linear plots of the amount-time curves of A, B, or C for the cases of (a) k1 = 0.1, k2 = 1, and k3 = 5, corresponding to the steady-state approximation, and (b) k1 = 10, k2 = 1, and k3 = 0.1, corresponding to the equilibrium approximation. The solid and dashed lines represent the exact and approximate solutions, respectively. The abscissa and ordinate denote time and the amount of each species, respectively, in arbitrary unit. See text for details.

Reference

1. Lowry TM, John WT. CCLXIX. Studies of dynamic isomerism. Part XII. The equations for two consecutive unimolecular changes. J Chem Soc Trans. 1910; 97:2634–2645. DOI: 10.1039/CT9109702634.

2. Chrastil J. Determination of the first-order consecutive reversible reaction kinetics. Comput Chem. 1993; 17:103–106. DOI: 10.1016/0097-8485(93)80035-C.

3. Binti Hasan NAS, Balasubramanian P. Exact Solution for the Kinetic Equations of First Order Reversible Reaction Systems through Flow Graph Theory Approach. Ind Eng Chem Res. 2013; 52:10594–10600. DOI: 10.1021/ie303501t.

4. DiStefano JJ 3rd. Concepts, properties, measurements, and computation of clearance rates of hormones and other substances in biological systems. Ann Biomed Eng. 1976; 4:302–319. PMID: 984535.

5. Hwang S, Kwan KC, Albert KS. A linear mode of reversible metabolism and its application to bioavailability assessment. J Pharmacokinet Biopharm. 1981; 9:693–709. PMID: 7341755.

6. Cheng H, Jusko WJ. Pharmacokinetics of reversible metabolic systems. Biopharm Drug Dispos. 1993; 14:721–766. PMID: 8298069.

7. Hallak HO, Wedlund PJ. Reversible metabolism of vitamin K-vitamin K epoxide: modeling considerations and limitations. J Pharmacokinet Biopharm. 1992; 20:1–18. PMID: 1588501.

8. Eriksson T, Björkman S, Roth B, Höglund P. Intravenous formulations of the enantiomers of thalidomide: pharmacokinetic and initial pharmacodynamic characterization in man. J Pharm Pharmacol. 2000; 52:807–817. PMID: 10933131.

9. Ebling WF, Jusko WJ. The determination of essential clearance, volume, and residence time parameters of recirculating metabolic systems: the reversible metabolism of methylprednisolone and methylprednisone in rabbits. J Pharmacokinet Biopharm. 1986; 14:557–599. PMID: 3820091.

10. Baillie TA, Adams WJ, Kaiser DG, Olanoff LS, Halstead GW, Harpootlian H, et al. Mechanistic studies of the metabolic chiral inversion of (R)-ibuprofen in humans. J Pharmacol Exp Ther. 1989; 249:517–523. PMID: 2724138.

11. Stoschitzky K, Lindner W, Egginger G, Brunner F, Obermayer-Pietsch B, Passath A, et al. Racemic (R,S)-propranolol versus half-dosed optically pure (S)-propranolol in humans at steady state: Hemodynamic effects, plasma concentrations, and influence on thyroid hormone levels. Clin Pharmacol Ther. 1992; 51:445–453. PMID: 1563214.

12. Volk L, Richardson W, Lau KH, Hall M, Lin SH. Steady state and equilibrium approximations in reaction kinetics. J Chem Educ. 1977; 54:95–97. DOI: 10.1021/ed054p95.

13. Cho S, Yoon YR. Understanding the pharmacokinetics of prodrug and metabolite. Transl Clin Pharmacol. 2018; 26:1–5. DOI: 10.12793/tcp.2018.26.1.

14. Rowland M, Tozer TN. Clinical pharmacokinetics and pharmacodynamics: concepts and applications. 4th ed. Philadelphia: Wolters Kluwer Health/Lippincott William & Wilkins;2011. p. 603–632.

15. Smith PC. Pharmacokinetics of drug metabolites. In : Pearson PG, Wienkers LC, editors. Handbook of drug metabolism. 2nd ed. New York: Informa Healthcare;2009. p. 17–59.

16. Mucientes AE, de la Peña MA. Kinetic Analysis of Parallel-Consecutive First-Order Reactions with a Reversible Step: Concentration–Time Integrals Method. J Chem Educ. 2009; 86:390–392. DOI: 10.1021/ed086p390.

17. Pang KS. A review of metabolite kinetics. J Pharmacokinet Biopharm. 1985; 13:633–662. PMID: 3914545.

18. de Campos ML, Padilha EC, Peccinini RG. A review of pharmacokinetic parameters of metabolites and prodrugs. Drug Metab Lett. 2014; 7:105–116. PMID: 24628402.

19. McDaniel DH, Smoot CR. Approximations in the kinetics of consecutive reactions. J Phys Chem. 1956; 60:966–969. DOI: 10.1021/j150541a035.

20. Pyun CW. Steady-state and equilibrium approximations in chemical kinetics. J Chem Educ. 1971; 48:194–196. DOI: 10.1021/ed048p194.

21. Atkinson Jr AJ. Compartment analysis of drug distribution. In : Atkinson AJ, Huang S-M, Lertora JJL, Markey SP, editors. Principles of Clinical Pharmacology. 3rd ed. Amsterdam: Academic Press;2012. p. 27–39.

22. Michaelis L, Menten ML. Die Kinetik der Invertinwirkung. Biochem Z. 1913; 49:333–369.

23. Michaelis L, Menten ML, Johnson KA, Goody RS. The Original Michaelis Constant: Translation of the 1913 Michaelis–Menten Paper. Biochemistry. 2011; 50:8264–8269. DOI: 10.1021/bi201284u. PMID: 21888353.

24. Briggs GE, Haldane JB. A note on the kinetics of enzyme action. Biochem J. 1925; 19:338–339. PMID: 16743508.