Transl Clin Pharmacol.  2016 Sep;24(3):119-123. 10.12793/tcp.2016.24.3.119.

Tips for the choice of initial estimates in NONMEM

• Han S
• Jeon S
• Yim DS

• KMID: 2351796
• DOI: http://doi.org/10.12793/tcp.2016.24.3.119

Abstract

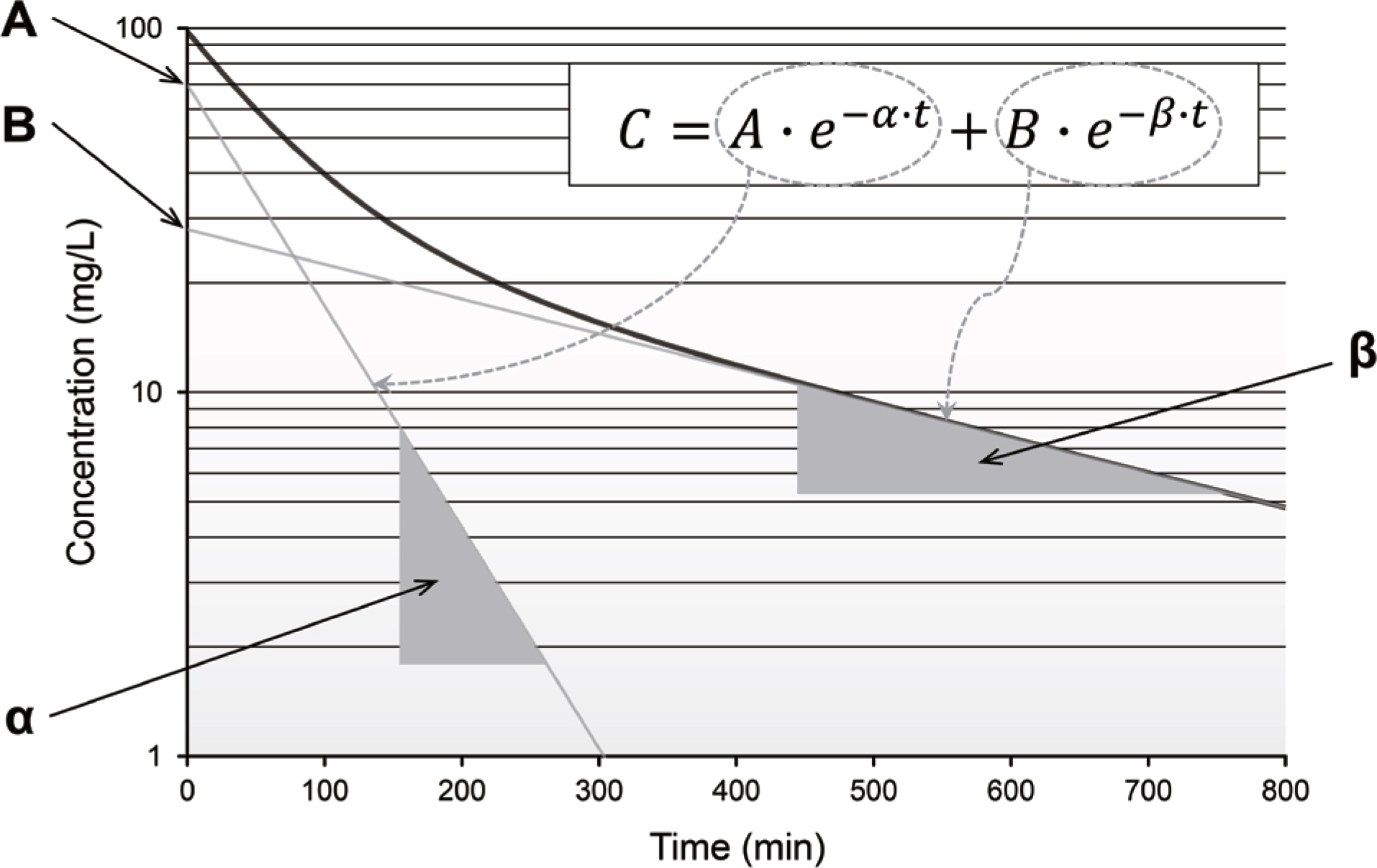
The importance of precise information and knowledge on the initial estimates (IEs) in modeling has not been paid its due attention so far. By focusing on the IE, this tutorial may serve as a practical guide for beginners in pharmacometrics. A 'good' set of IEs rather than arbitrary values is required because the IEs where NONMEM kicks off its estimation may influence the subsequent objective function minimization. To provide NONMEM with acceptable IEs, modelers should understand the exact meaning of THETA, OMEGA and SIGMA based on physiology. In practice, problems related to the value of the IE are more likely to occur for THETAs rather than the random-effect terms. Because it is almost impossible for a modeler to give a precise IE for OMEGAs at the beginning, it may be a good practice to start at relatively small IEs for them. NONMEM may fail to converge when too small IEs are provided for residual error parameters; thus, it is recommended to give sufficiently large values for them. The understandings on the roles, meanings and implications of IEs even help modelers in troubleshooting situations which frequently occur over the whole modeling process.

Keyword

NONMEM; initial estimate; pharmacometrics; pharmacokinetic-pharmacodynamic model

MeSH Terms

Physiology

Figure

• 

  Figure 1. Simple presentation of the Newton–Raphson method. X1 is the set of initial estimates (starting point) and Xi is the set of parameter estimates at each iteration step. (Redrawn based on the figure in reference [3])

• 

  Figure 2. Example of functions having multiple minima. (Redrawn based on the figure in reference [3])

• 

  Figure 3. Sum of exponentials for a two-compartment model and macro constants. (Redrawn based on the figure in reference [4])

Reference

1.Beal SL., Sheiner LB. NONMEM Users Guide –Part I. Users Basic Guide. NONMEM Project Group. 1989.

2.Choi K., Yim DS. Statistical basis for pharmacometrics: maximum likelihood estimator and its asymptotics. Transl Clin Pharmacol. 2015. 23:8–14. DOI: doi: 10.12793/tcp.2015.23.1.8.

3.Nonlinear models and regression. Bonate PL, editor. (ed). Pharmacokinetic-pharmacodynamic modeling and simulation. 2nd ed.Springer Science+Bu-siness Media;LLC, New York: 2011. p. 101–130.

4.Pharmacokinetic Concepts. In: Gabrielsson J, Weiner D. (ed) Pharmacokinetic & pharmacodynamic data analysis. 5th ed.apotekarsocieteten, Stockholm, Sweden;2016. p. 13–198.

5.Pharmacodynamic Concepts. In: Gabrielsson J, Weiner D. (ed) Pharmacokinetic & pharmacodynamic data analysis. 5th ed.apotekarsocieteten, Stockholm, Sweden;2016. p. 199–332.