Transl Clin Pharmacol.  2018 Mar;26(1):39-47. 10.12793/tcp.2018.26.1.39.

Comparison of various estimation methods for the parameters of Michaelis-Menten equation based on in vitro elimination kinetic simulation data

• Cho YS
• Lim HS

• KMID: 2420306
• DOI: http://doi.org/10.12793/tcp.2018.26.1.39

Abstract

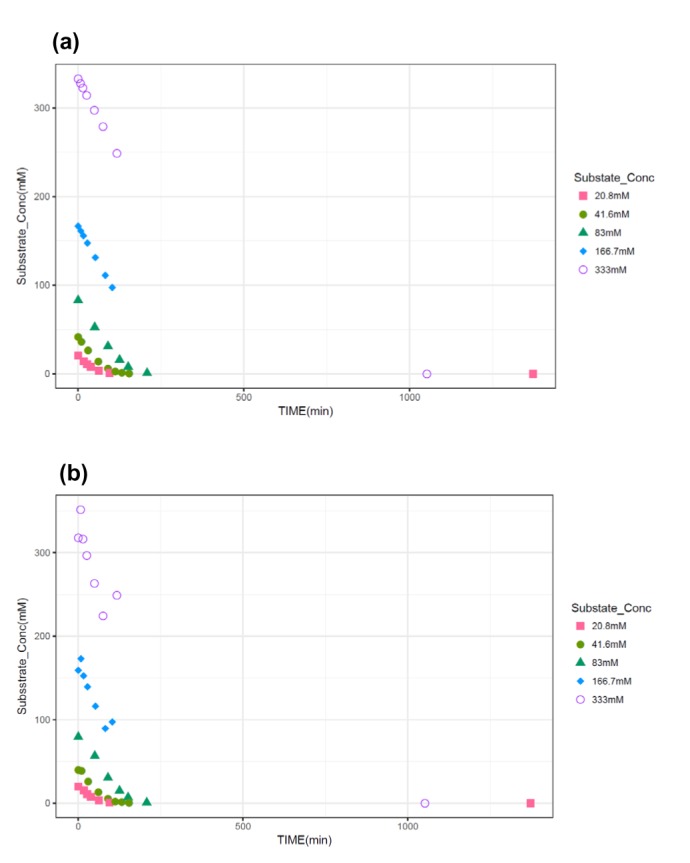
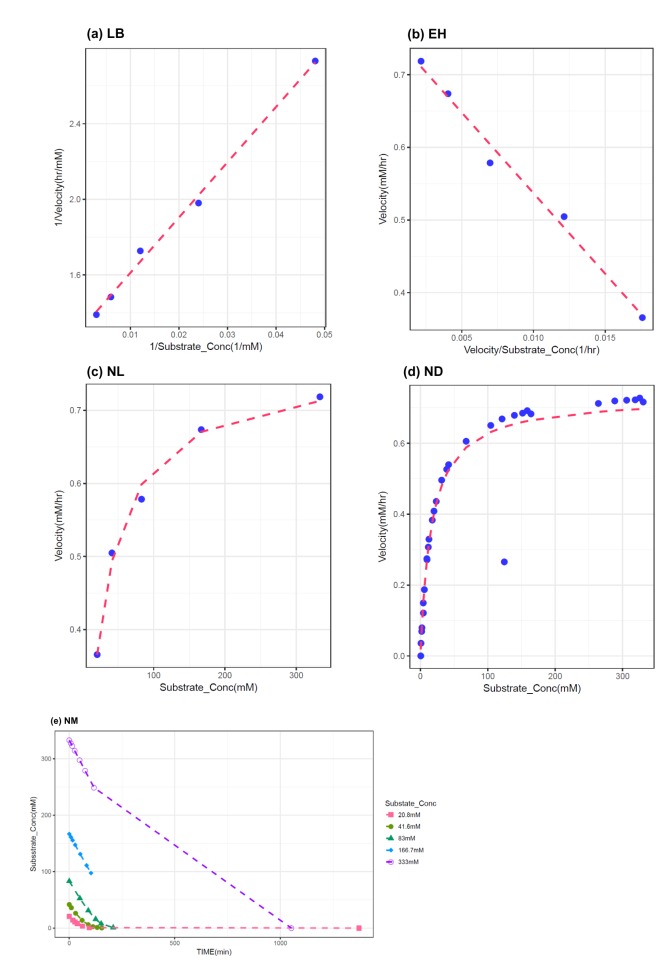
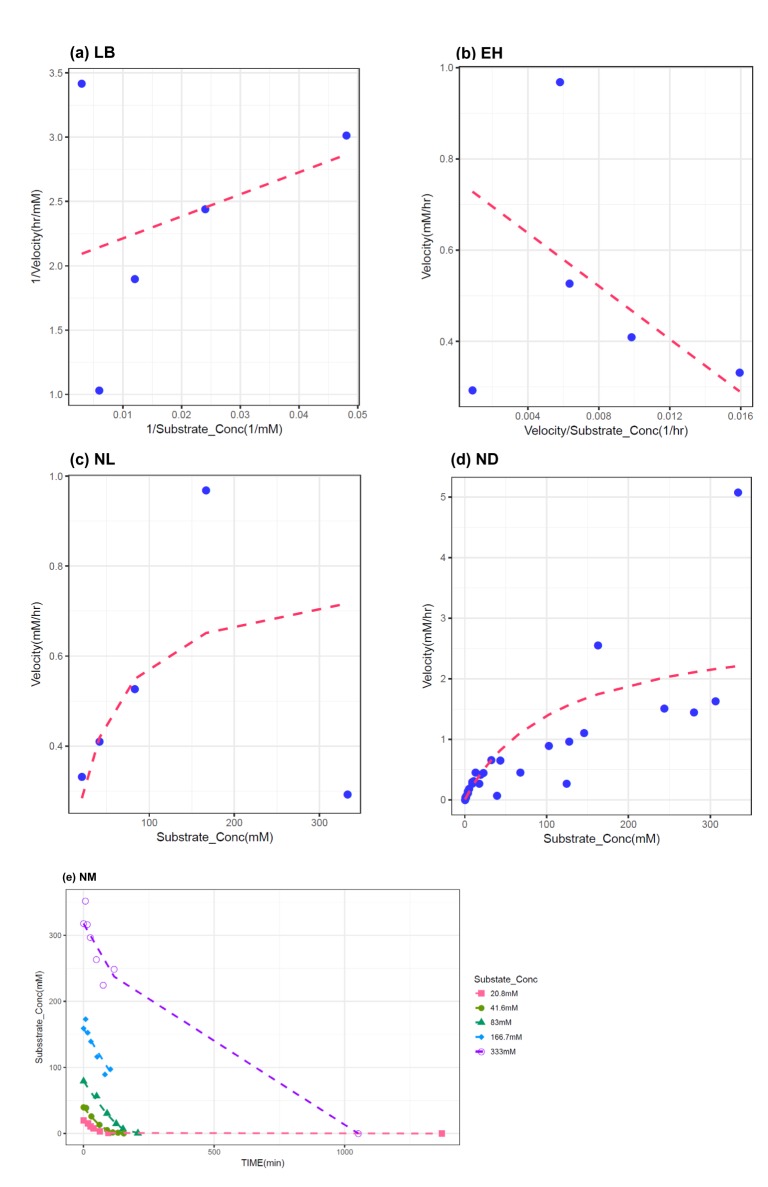
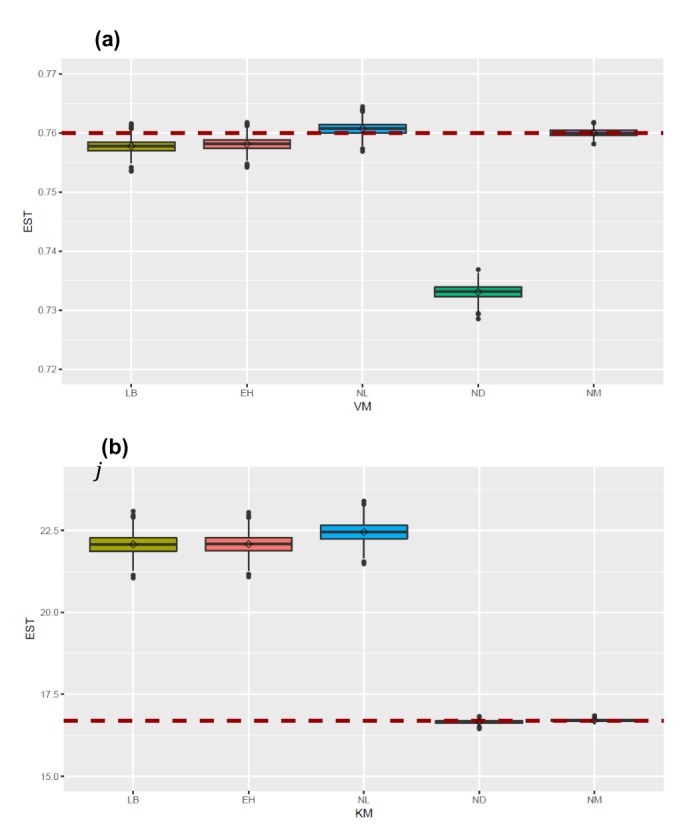
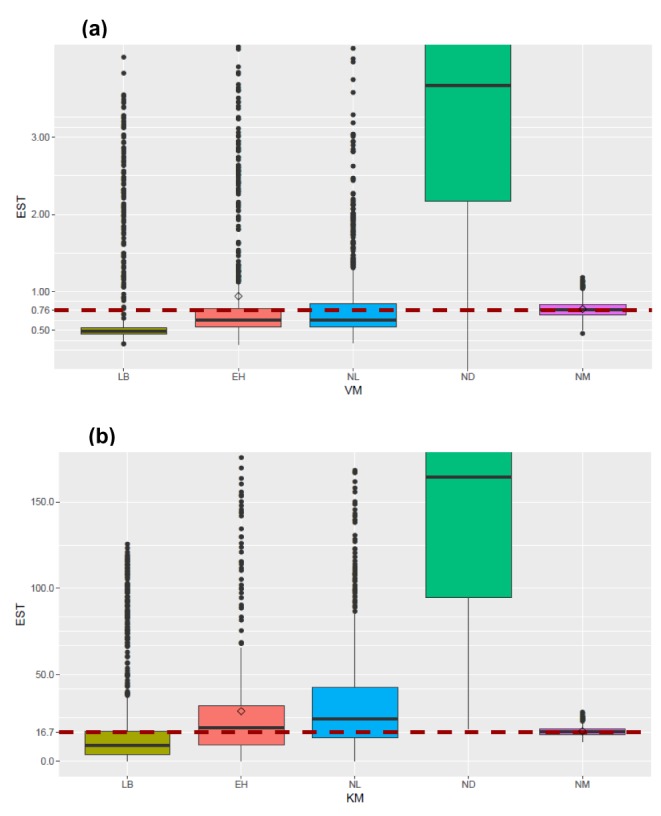
The Michaelis-Menten equation is one of the best-known models describing the enzyme kinetics of in vitro drug elimination experiments, and takes a form of equation relating reaction rate (V) to the substrate concentration ([S]) via the maximum reaction rate (Vmax) and the Michaelis constant (Km). The current study was conducted to compare the accuracy and precision of the parameter estimates in the Michaelis-Menten equation from various estimation methods using simulated data. One thousand replicates of simulated [S] over serial time data were generated using the results of a previous study, incorporating additive or combined error models as a source of random variables in the Monte-Carlo simulation using R. From each replicate of simulated data, Vmax and Km were estimated by five different methods, including traditional linearization methods and nonlinear ones without linearization using NONMEM. The relative accuracy and precision of the estimated parameters were compared by the median values and their 90% confidence intervals. Overall, Vmax and Km estimation by nonlinear methods (NM) provided the most accurate and precise results from the tested 5 estimation methods. The superiority of parameter estimation by NM was even more evident in the simulated data incorporating the combined error model. The current simulation study suggests that NMs using a program such as NONMEM provide more reliable and accurate parameter estimates of the Michaelis-Menten equation than traditional linearization methods in in vitro drug elimination kinetic experiments.

Keyword

Simulation; Michaelis-Menten equation; Nonlinear estimation method; in vitro drug elimination kinetic experiment; NONMEM

MeSH Terms

In Vitro Techniques*
Kinetics
Methods*

Figure

• 

  Figure 1 The substrate concentration ([S])-time profiles of randomly selected simulation data incorporating additive error (a) or combined error (b). The simulated data is shown as differently shaped points for each initial [S].

• 

  Figure 2 Curves fitted using 5 different fitting methods, a)-e), for the selected simulation data incorporating additive error in Figure 1. The simulated data are shown as points and the prediction using each fitting methods are shown as dashed lines in a)-e). LB is Lineweaver-Burk plot, EH is Eadie-Hofstee plot, NL is nonlinear regression to the initial velocity (Vi) versus substrate concentration (Vi-[S]) data, ND is nonlinear regression to the velocity versus substrate concentration (V-[S]) data directly transformed from [S]-time data, and NM is nonlinear direct fitting method to substrate concentration ([S])-time data.

• 

  Figure 3 Curves fitted using 5 different fitting methods, a)-e), for the selected simulation data incorporating combined error in Figure 1. The simulated data are shown as points and the prediction using each fitting methods are shown as dashed lines in a)-e). LB is Lineweaver-Burk plot, EH is Eadie-Hofstee plot, NL is nonlinear regression to the initial velocity (Vi) versus substrate concentration (Vi-[S]) data, ND is nonlinear regression to the velocity versus substrate concentration (V-[S]) data directly transformed from [S]-time data, and NM is nonlinear direct fitting method to substrate concentration ([S])-time data.

• 

  Figure 4 Box-and-whisker plot of Vmax (a) and Km (b) estimated by 5 different fitting methods for simulation data incorporating additive error. Red dashed lines denote true parameter values. LB is the Lineweaver-Burk plot, EH is the Eadie-Hofstee plot, NL is nonlinear regression to the initial velocity (Vi) versus substrate concentration (Vi-[S]) data, ND is nonlinear regression to the velocity versus substrate concentration (V-[S]) data directly transformed from [S]-time data, and NM is nonlinear direct fitting method to substrate concentration ([S])-time data.

• 

  Figure 5 Box-and-whisker plot of Vmax (a) and Km (b) estimated by 5 different fitting methods for simulation data incorporating combined error. Red dashed lines denote true parameter values. LB is Lineweaver-Burk plot, EH is Eadie-Hofstee plot, NL is nonlinear regression to the initial velocity (Vi) versus substrate concentration (Vi-[S]) data, ND is nonlinear regression to the velocity versus substrate concentration (V-[S]) data directly transformed from [S]-time data, and NM is nonlinear direct fitting method to substrate concentration ([S])-time data.

Reference

1. Michaelis L, Menten ML, Johnson KA, Goody RS. The original Michaelis constant: translation of the 1913 Michaelis-Menten paper. Biochemistry. 2011; 50:8264–8269. DOI: 10.1021/bi201284u. PMID: 21888353.

2. Cornish-Bowden A. The origins of enzyme kinetics. FEBS Lett. 2013; 587:2725–2730. DOI: 10.1016/j.febslet.2013.06.009. PMID: 23791665.

3. Johnson KA, Simpson ZB, Blom T. Global kinetic explorer: a new computer program for dynamic simulation and fitting of kinetic data. Anal Biochem. 2009; 387:20–29. DOI: 10.1016/j.ab.2008.12.024. PMID: 19154726.

4. Kuzmic P. Program DYNAFIT for the analysis of enzyme kinetic data: application to HIV proteinase. Anal Biochem. 1996; 237:260–273. PMID: 8660575.

5. Barshop BA, Wrenn RF, Frieden C. Analysis of numerical methods for computer simulation of kinetic processes: development of KINSIM--a flexible, portable system. Anal Biochem. 1983; 130:134–145. PMID: 6688159.

6. Cornish-Bowden A. Fundamentals of Enzyme Kinetics. 4th ed. Wiley-Blackwell: New York;2012. p. 16–38.

7. Fersht AR. Structure and mechanism in protein science. New York: W. H. Freedman;1999. p. 108–110.

8. Johnson KA. A century of enzyme kinetic analysis, 1913 to 2013. FEBS Lett. 2013; 587:2753–2766. DOI: 10.1016/j.febslet.2013.07.012. PMID: 23850893.

9. Bae KS, Yim DS. R-based reproduction of the estimation process hidden behind NONMEM® Part 2: First-order conditional estimation. Transl Clin Pharmacol. 2016; 24:161–168.

10. Hofstee BH. Non-inverted versus inverted plots in enzyme kinetics. Nature. 1959; 184:1296–1298. PMID: 14402470.

11. Nelatury SR, Nelatury CF, Vagula MC. Parameter Estimation in Different Enzyme Reactions. Adv Enzyme Res. 2014; 2:14–26. DOI: 10.4236/aer.2014.21002.

12. Kemmer G, Keller S. Nonlinear least-squares data fitting in Excel spreadsheets. Nat Protoc. 2010; 5:267–281. DOI: 10.1038/nprot.2009.182. PMID: 20134427.

13. Page A. A non-linear regression program in BASIC for estimating Km and Vmax. Comput Appl Biosci. 1987; 3:49–51. PMID: 3453214.

14. Marszalek J, Kostrowicki J, Spychala J. LEHM: a convenient non-linear regression microcomputer prog ram for fitting Michaelis-Menten and Hill models to enzyme kinetic data. Comput Appl Biosci. 1989; 5:239–240. PMID: 2766012.