Yonsei Med J.  2005 Apr;46(2):275-283. 10.3349/ymj.2005.46.2.275.

Computational Analysis of Tumor Angiogenesis Patterns Using a Two-dimensional Model

• Shim EB
• Kwon YG
• Ko HJ

• KMID: 1734055
• DOI: http://doi.org/10.3349/ymj.2005.46.2.275

Abstract

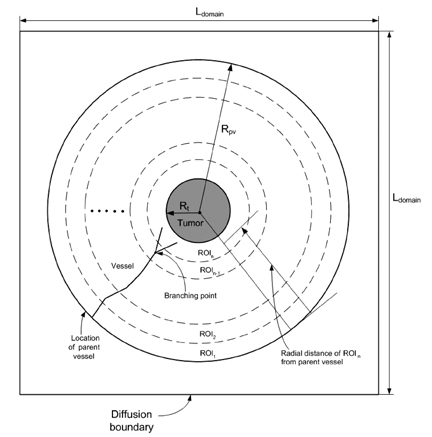
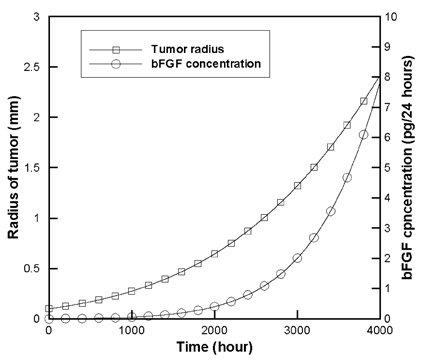
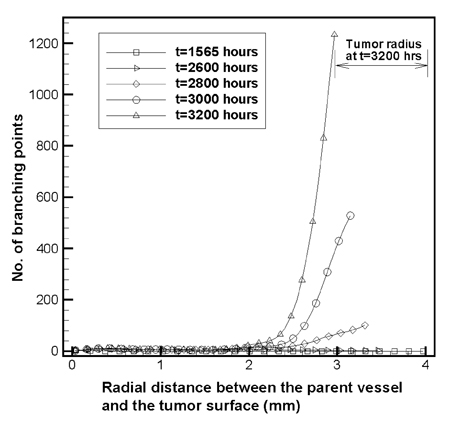
Tumor angiogenesis was simulated using a two-dimensional computational model. The equation that governed angiogenesis comprised a tumor angiogenesis factor (TAF) conservation equation in time and space, which was solved numerically using the Galerkin finite element method. The time derivative in the equation was approximated by a forward Euler scheme. A stochastic process model was used to simulate vessel formation and vessel elongation towards a paracrine site, i.e., tumor-secreted basic fibroblast growth factor (bFGF). In this study, we assumed a two-dimensional model that represented a thin (1.0mm) slice of the tumor. The growth of the tumor over time was modeled according to the dynamic value of bFGF secreted within the tumor. The data used for the model were based on a previously reported model of a brain tumor in which four distinct stages (multicellular spherical, first detectable lesion, diagnosis, and death of the virtual patient) were modeled. In our study, computation was not continued beyond the 'diagnosis' time point to avoid the computational complexity of analyzing numerous vascular branches. The numerical solutions revealed that no bFGF remained within the region in which vessels developed, owing to the uptake of bFGF by endothelial cells. Consequently, a sharp declining gradient of bFGF existed near the surface of the tumor. The vascular architecture developed numerous branches close to the tumor surface (the brush-border effect). Asymmetrical tumor growth was associated with a greater degree of branching at the tumor surface.

Keyword

Tumor growth; angiogenesis; computational modeling; basic fibroblast growth factor

MeSH Terms

Computer Simulation
Fibroblast Growth Factor 2/metabolism
Humans
*Models, Biological
Neoplasms/*blood supply/metabolism
Neovascularization, Pathologic/*physiopathology
Research Support, Non-U.S. Gov't

Figure

• 

  Fig. 1 Two-dimensional model geometry for the standard case of symmetrical tumor growth. Radii are depicted as described in the text. To facilitate computation, the geometric growth of the central (gray) tumor circle was not calculated. This figure also illustrates the region of interest (ROI) and branching point.

• 

  Fig. 2 Two-dimensional model geometry for asymmetrical tumor growth.

• 

  Fig. 3 Radius of the tumor and concentration of basic fibroblast growth factor (bFGF) over time.

• 

  Fig. 4 Contours of concentration gradient for bFGF (relative to bFGF concentration for a tumor radius of 1.0 mm at t=2,590 h) over time for the standard case of symmetrical tumor growth. (A) t=1,656 h (spherical growth stage). (B) t=2,600 h. (C) t=3,000 h.

• 

  Fig. 5 Vessel structures over time for the standard case of symmetrical growth (Smax=0.5). (A) t=1,656 h (spherical growth stage). (B) t=2,600 h. (C) t=3,200 h.

• 

  Fig. 6 Number of branching points versus the ROI, i.e., the radial distance between the parent vessel and the tumor surface.

• 

  Fig. 7 Total vessel length over time for the standard case of symmetrical tumor growth.

• 

  Fig. 8 Contours of concentration gradient for bFGF (relative to bFGF concentration for a tumor radius of 1.0 mm at t=2,590 h) at t=3,000 h for asymmetrical growth.

• 

  Fig. 9 Vessel structures over time for the standard case of symmetrical growth at t=3,200 h.

Reference

1. Folkman J. Angiogenesis in cancer, vascular, rheumatoid and other disease. Nat Med. 1995. 1:21–31.

2. Chaplain MAJ. Avascular growth, angiogenesis and vascular growth in solid tumours: the mathematical modelling of the stages of tumour development. Math Comput Model. 1996. 23:47–87.

3. Chaplain MAJ, Anderson ARA. The mathematical modelling, simulation and prediction of tumour-induced angiogenesis. Invasion Metastasis. 1997. 16:222–234.

4. Gazit Y, Berk DA, Leunig M, Baxter LT, Jain RK. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys Rev Lett. 1995. 75:2428–2431.

5. Tong S, Yuan F. Numerical simulations of angiogenesis in the cornea. Microvasc Res. 2001. 61:14–27.

6. Kansal AR, Torquato S, Harsh GR, Chiocca EA, Deisboeck TS. Simulated brain tumor growth dynamics using a three-dimensional cellular automation. J Theor Biol. 2000. 203:1–18.

7. Takahashi JA, Fukumuto M, Igarashi K, Oda Y, Kikuchi H, Hatanaka M. Correlation of basic fibroblast growth factor expression levels with the degree of malignancy and vascularity in human gliomas. J Neurosurg. 1992. 76:792–798.

8. Zagzag D, Miller DC, Sato Y, Rifkin DB, Burstein DE. Immunohistochemical localization of basic fibroblast growth factor in astrocytomas. Cancer Res. 1990. 50:7393–7398.

9. Sato Y, Murphy PR, Sato R, Friesen HG. Fibroblast growth factor release by bovine endothelial cells and human astrocytoma cells in culture is density dependent. Mol Endocrinol. 1989. 3:744–748.

10. Kershaw D. The incomplete Cholesky-conjugate gradient method for the iterative solution of linear equations. J Comput Phys. 1978. 26:43–65.

11. Stokes CL, Lauffenburger DA. Analysis of the roles of microvessel endothelial cell random motility and chemotaxis in angiogenesis. J Theor Biol. 1991. 152:377–403.