J Dent Rehabil Appl Sci.  2020 Jun;36(2):112-120. 10.14368/jdras.2020.36.2.112.

Comparison of the outcomes of three-dimensional finite element analysis under arbitrary and realistic occlusal loading conditions in mandibular posterior region

• Lee W
• Alom G
• Kim MS
• Park YS
• Lim YJ
• Kim MJ
• Kwon HB

• KMID: 2503807
• DOI: http://doi.org/10.14368/jdras.2020.36.2.112

Abstract

Purpose
The purpose of this study was to compare the biomechanical outcome in the mandibular posterior region between two different loading conditions by finite element analysis.
Materials and Methods
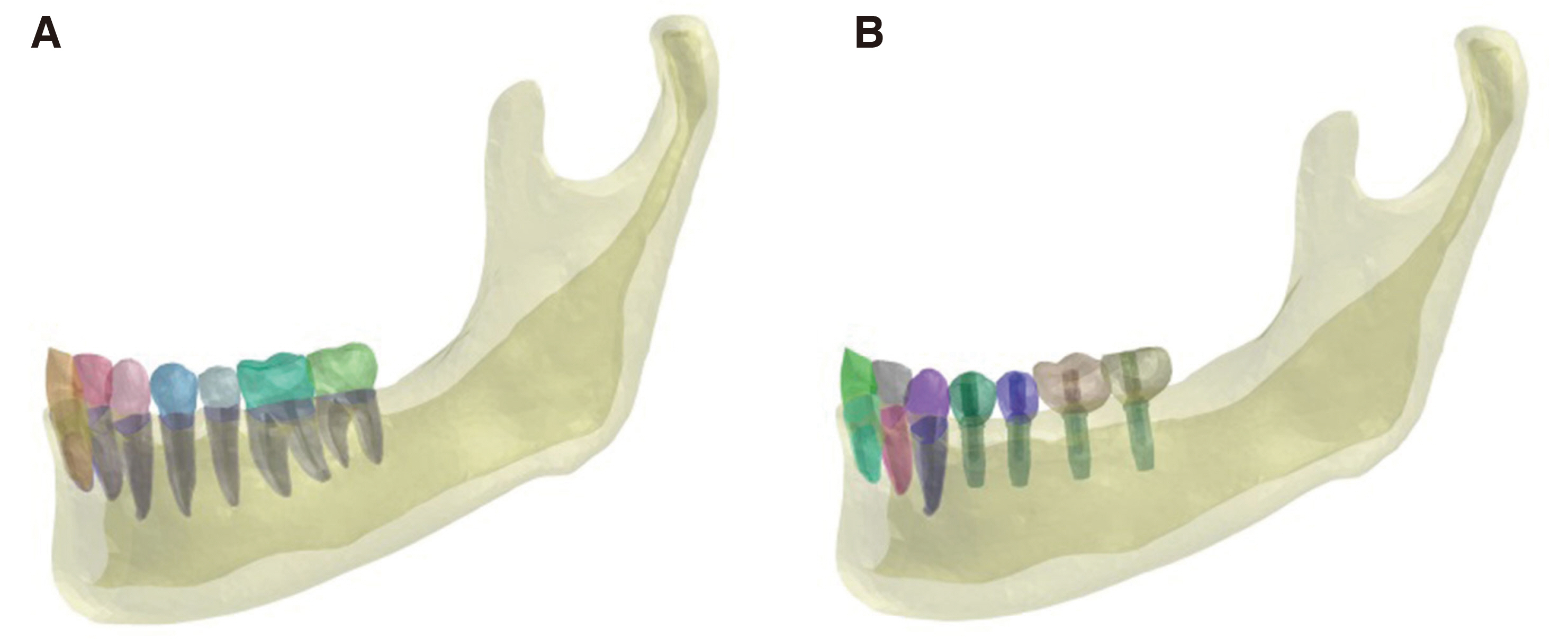
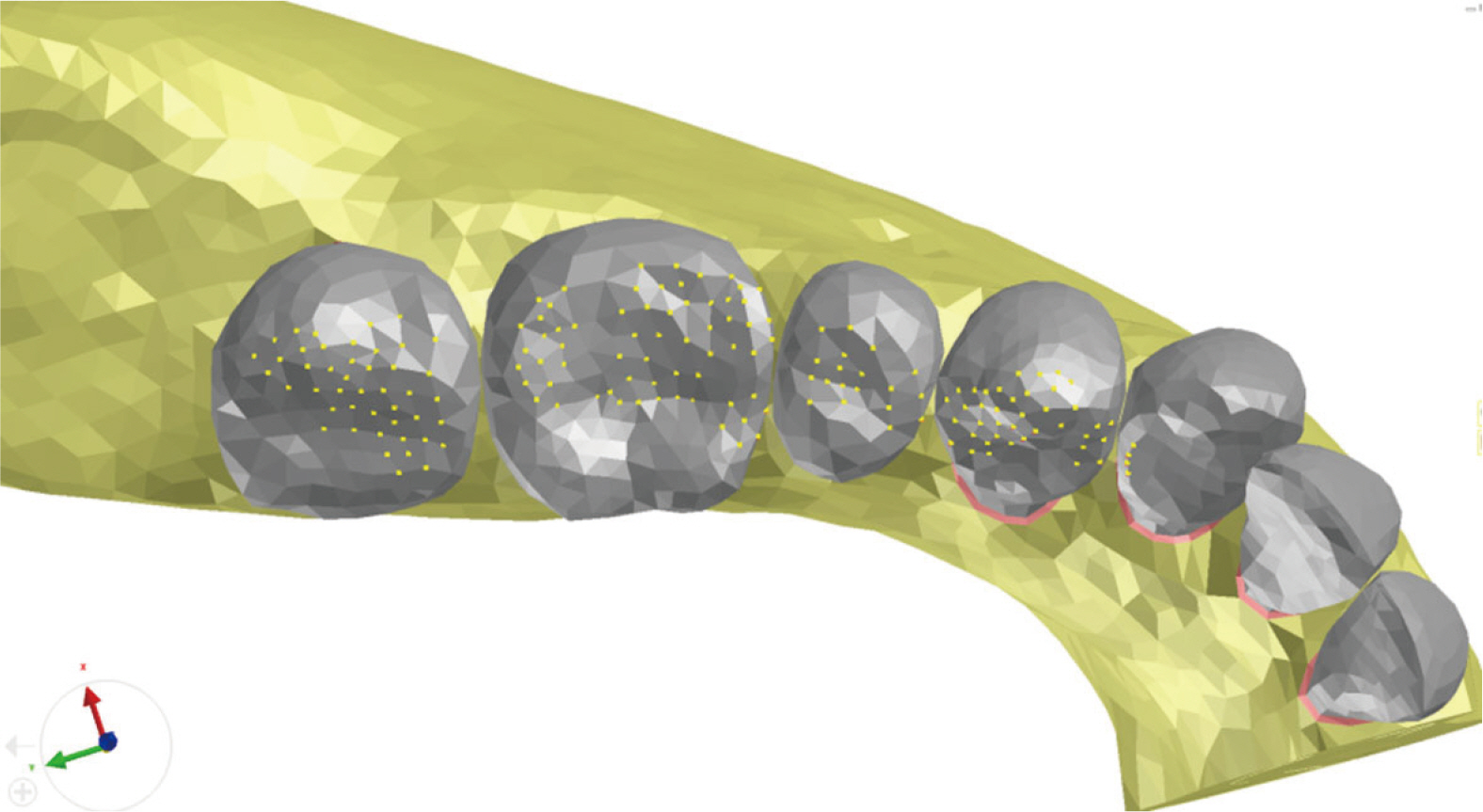
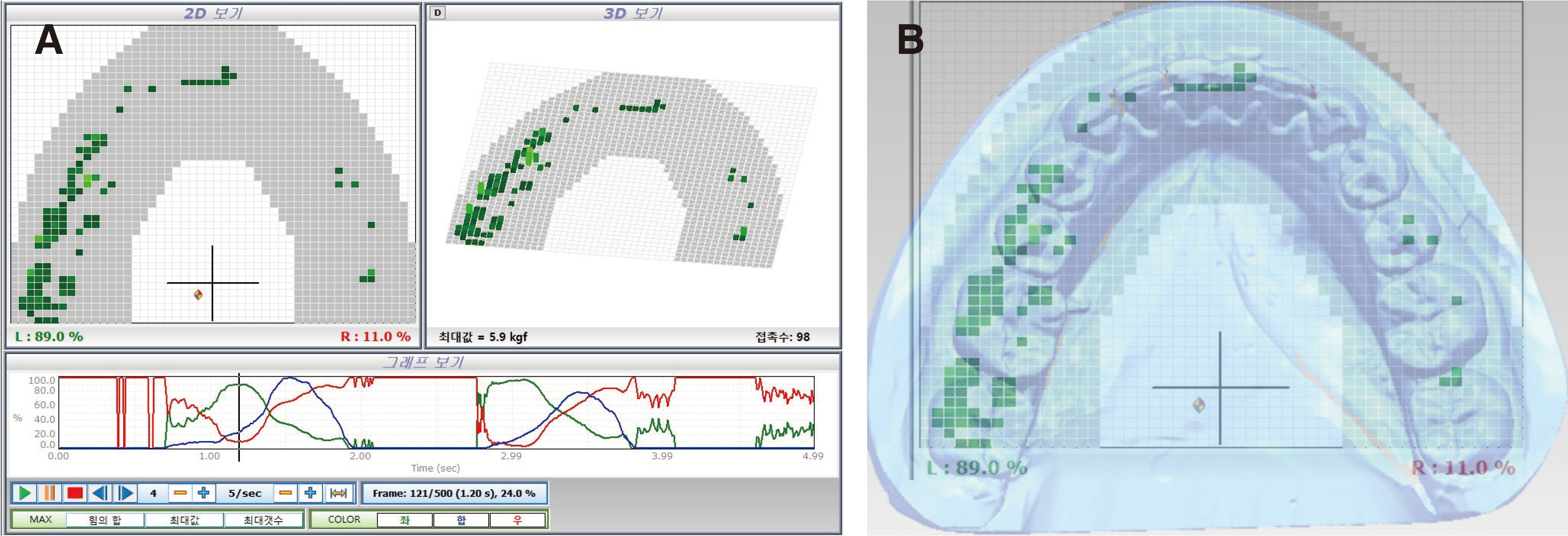
The mandibular posterior teeth model and the implant model were generated for the study. And 2 different types of loading conditions were provided: Arbitrary occlusion and natural occlusion obtained from the digital occlusal analyzer, Accura (Accura, Dmetec Co. Ltd., Seoul, Korea). Total load of 100 N was evenly distributed over arbitrary occlusion points, and 100 N load was differentially distributed over natural occlusion points according to Accura data. The biomechanical outcome was evaluated by the finite element analysis software.
Results
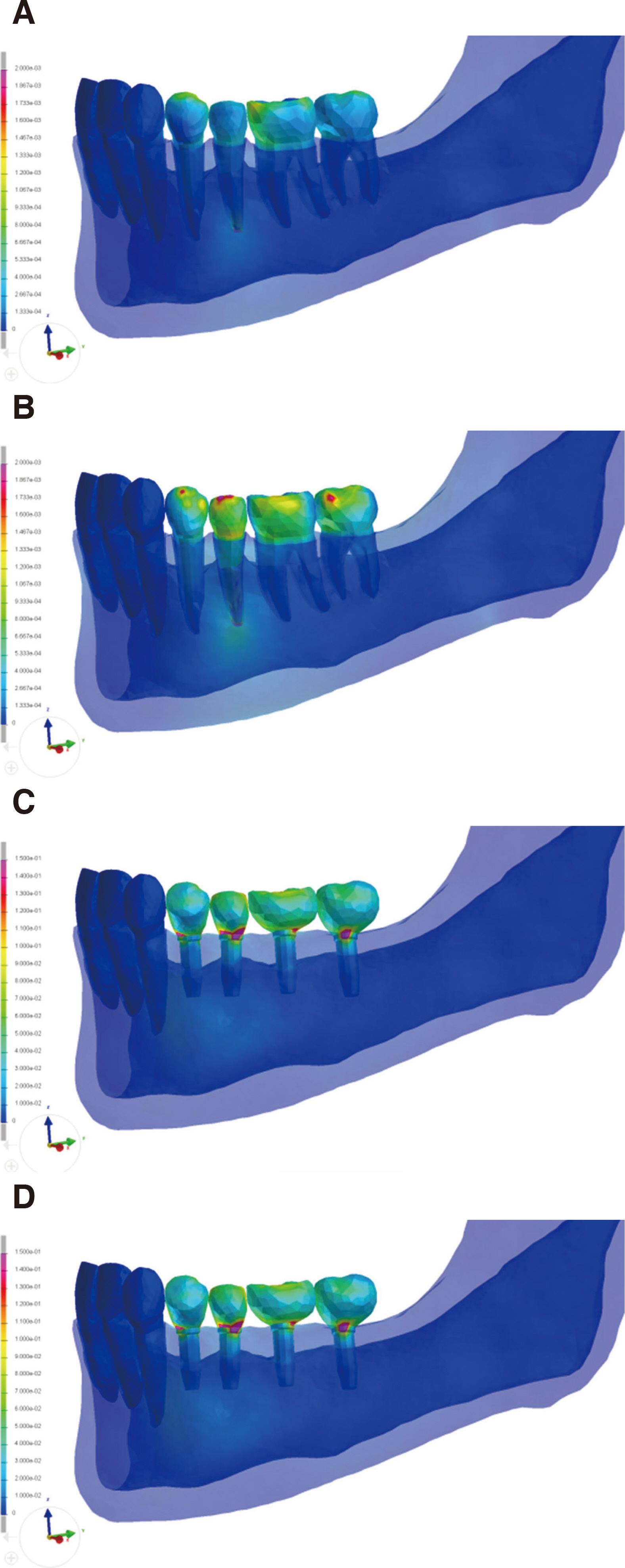
The result of finite element analysis showed considerable difference in both von Mises stress pattern and displacement under different loading conditions.
Conclusion
In finite element analysis, it is recommended to simulate a realistic occlusal loading pattern that is based on accurate measurement.

Keyword

digital occlusal analyzer; occlusion; finite element analysis

Figure

• 

  Fig. 1 Mesh models generated for finite element analysis. (A) Natural teeth model which consist of the mandibular cortical bone, cancellous bone, periodontal ligament, and teeth, (B) Implant model which consist of the mandibular cortical bone, cancellous bone, implant, abutment screw, abutment, and crown.

• 

  Fig. 2 Arbitrary occlusion setup. Yellow points are arbitrary occlusal points designated on premolar and molar region.

• 

  Fig. 3 Natural occlusion setup. (A) Natural occlusion data acquisition by Accura, (B) Based on natural occlusion data, occlusal points were determined by superimposition of Accura data and model geometry.

• 

  Fig. 4 Von Mises stress distribution pattern. (A) NA model, (B) NN model, (C) IA model, (D) IN model.

Reference

References

1. Geng JP, Tan KB, Liu GR. 2001; Application of finite element analysis in implant dentistry: a review of the literature. J Prosthet Dent. 85:585–98. DOI: 10.1067/mpr.2001.115251. PMID: 11404759.

2. DeTolla DH, Andreana S, Patra A, Buhite R, Comella B. 2000; Role of the finite element model in dental implants. J Oral Implantol. 26:77–81. DOI: 10.1563/1548-1336(2000)026<0077:TROTFE>2.3.CO;2.

3. Trivedi S. 2014; Finite element analysis: a boon to dentistry. J Oral Biol Craniofac Res. 4:200–3. DOI: 10.1016/j.jobcr.2014.11.008. PMID: 25737944. PMCID: PMC4306993.

4. Shetty P, Hegde AM, Rai K. 2010; Finite element method-an effective research tool for dentistry. J Clin Pediatr Dent. 34:281–5. DOI: 10.17796/jcpd.34.3.yu44334815546435. PMID: 20578669.

5. Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. 2004; The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: a three-dimensional finite element study. J Prosthet Dent. 91:144–50. DOI: 10.1016/j.prosdent.2003.10.018. PMID: 14970760.

6. Hernández-Vázquez RA, Romero-Ángeles B, Urriolagoitia-Sosa G, Vázquez-Feijoo JA, Vázquez-López ÁJ, Urriolagoitia-Calderón G. 2018; Numerical analysis of masticatory forces on a lower first molar considering the contact between dental tissues. Appl Bionic Biomech. 2018:4196343. DOI: 10.1155/2018/4196343. PMID: 29849758. PMCID: PMC5914157.

7. Benazzi S, Grosse IR, Gruppioni G, Weber GW, Kullmer O. 2014; Comparison of occlusal loading conditions in a lower second premolar using three-dimensional finite element analysis. Clin Oral Investig. 18:369–75. DOI: 10.1007/s00784-013-0973-8. PMID: 23504207.

8. Brune A, Stiesch M, Eisenburger M, Greuling A. 2019; The effect of different occlusal contact situations on peri-implant bone stress - a contact finite element analysis of indirect axial loading. Mater Sci Eng C Mater Biol Appl. 99:367–73. DOI: 10.1016/j.msec.2019.01.104. PMID: 30889710.

9. Röehrle O, Saini H, Ackland DC. 2018; Occlusal loading during biting from an experimental and simulation point of view. Dent Mater. 34:58–68. DOI: 10.1016/j.dental.2017.09.005. PMID: 29017762.

10. Chang Y, Tambe AA, Maeda Y, Wada M, Gonda T. 2018; Finite element analysis of dental implants with validation: to what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Int J Implant Dent. 4:7. DOI: 10.1186/s40729-018-0119-5. PMID: 29516219. PMCID: PMC5842167.

11. De Jager N, de Kler M, van der Zel JM. 2006; The influence of different core material on the FEA-determined stress distribution in dental crowns. Dent Mater. 22:234–42. DOI: 10.1016/j.dental.2005.04.034. PMID: 16099031.

12. Kondo T, Wakabayashi N. 2009; Influence of molar support loss on stress and strain in premolar periodontium: a patient-specific FEM study. J Dent. 37:541–8. DOI: 10.1016/j.jdent.2009.03.015. PMID: 19380187.

13. Rand A, Stiesch M, Eisenburger M, Greuling A. 2017; The effect of direct and indirect force transmission on peri-implant bone stress - a contact finite element analysis. Comput Methods Biomech Biomed Engin. 20:1132–9. DOI: 10.1080/10255842.2017.1338691. PMID: 28622020.

14. Cailleteau JG, Rieger MR, Akin JE. 1992; A comparison of intracanal stresses in a post-restored tooth utilizing the finite element method. J Endodont. 18:540–4. DOI: 10.1016/S0099-2399(06)81210-0.

15. Papavasiliou G, Kamposiora P, Bayne SC, Felton DA. 1996; Three-dimensional finite element analysis of stress-distribution around single tooth implants as a function of bony support prosthesis type and loading during function. J Prosthet Dent. 76:633–40. DOI: 10.1016/S0022-3913(96)90442-4.

16. Ausiello P, Apicella A, Davidson CL. 2002; Effect of adhesive layer properties on stress distribution in composite restorations - a 3D finite element analysis. Dent Mater. 18:295–303. DOI: 10.1016/S0109-5641(01)00042-2.

17. Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. 2004; The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: a three-dimensional finite element study. J Prosthet Dent. 91:144–50. DOI: 10.1016/j.prosdent.2003.10.018. PMID: 14970760.

18. Lanza A, Aversa R, Rengo S, Apicella D, Apicella A. 2005; 3D FEA of cemented steel glass and carbon posts in a maxillary incisor. Dent Mater. 21:709–15. DOI: 10.1016/j.dental.2004.09.010. PMID: 16026666.

19. Mozayek RS, Allaf M, Abuharb MB. 2016; Efficacy of adding a supporting implant in stress distribution of long-span fixed partial dentures: a 3D finite element analysis. J Dent Res Dent Clin Dent Prospects. 10:81–6. DOI: 10.15171/joddd.2016.013. PMID: 27429723. PMCID: PMC4946000.

20. Jeong MY, Lim YJ, Kim MJ, Kwon HB. 2020; Comparison of two computerized occlusal analysis systems for indicating occlusal contacts. J Adv Prosthodont. 12:49–54. DOI: 10.4047/jap.2020.12.2.49. PMID: 32377316. PMCID: PMC7183850.

21. Coolidge ED. 1937; The thickness of the human periodontal membrane. J Am Dent Assoc. 24:1260–70. DOI: 10.14219/jada.archive.1937.0229.

22. Yoshida N, Koga Y, Peng CL, Tanaka E, Kobayashi K. 2001; In vivo measurement of the elastic modulus of the human periodontal ligament. Med Eng Phy. 23:567–72. DOI: 10.1016/S1350-4533(01)00073-X.

23. Cattaneo PM, Dalstra M, Melsen B. 2005; The finite element method: a tool to study orthodontic tooth movement. J Dent Res. 84:428–33. DOI: 10.1177/154405910508400506. PMID: 15840778.

24. Moroi HH, Okimoto K, Moroi R, Terada Y. 1993; Numeric approach to the biomechanical analysis of thermal effects in coated implants. Int J Prosthodont. 6:564–72.

25. Sano H, Ciucchi B, Matthews WG, Pashley DH. 1994; Tensile properties of mineralized and demineralized human and bovine dentin. J Dent Res. 73:1205–11. DOI: 10.1177/00220345940730061201. PMID: 8046110.

26. Farah JW, Craig RG, Meroueh KA. 1989; Finite element analysis of three- and four-unit bridges. J Oral Rehabil. 16:603–11. DOI: 10.1111/j.1365-2842.1989.tb01384.x. PMID: 2689617.

27. Jones ML, Hickman J, Middleton J, Knox J, Volp C. 2001; A validated finite element method study of orthodontic tooth movement in the human subject. J Orthod. 28:29–38. DOI: 10.1093/ortho/28.1.29. PMID: 11254801.

28. Tanne K, Yoshida S, Kawata T, Sasaki A, Knox J, Jones ML. 1998; An evaluation of the biomechanical response of the tooth and periodontium to orthodontic forces in adolescent and adult subjects. Br J Orthod. 25:109–15. DOI: 10.1093/ortho/25.2.109. PMID: 9668993.

29. Toms SR, Eberhardt AW. 2003; A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am J Orthod Dentofacial Orthop. 123:657–65. DOI: 10.1016/S0889-5406(03)00164-1.

30. Jung WK, Lee WS, Kwon HB. 2019; Effects of abutment screw preload in two implant connection systems: a 3D finite element study. J Prosthet Dent. 122:474.e1–e8. DOI: 10.1016/j.prosdent.2019.04.025. PMID: 31590980.

31. Silva GC, Cornacchia TM, de Magalhães CS, Bueno AC, Moreira AN. 2014; Biomechanical evaluation of screw-and cement-retained implant-supported prostheses: a nonlinear finite element analysis. J Prosthet Dent. 112:1479–88. DOI: 10.1016/j.prosdent.2014.06.010. PMID: 25062583.

32. Quaresma SET, Cury PR, Sendyk WR, Sendyk C. 2008; A finite element analysis of two different dental implants: stress distribution in the prosthesis, abutment, implant, and supporting bone. J Oral Implantol. 34:1–6. DOI: 10.1563/1548-1336(2008)34[1:AFEAOT]2.0.CO;2.

33. Wataha JC. 2002; Alloys for prosthodontic restorations. J Prosthet Dent. 87:351–63. DOI: 10.1067/mpr.2002.123817. PMID: 12011845.

34. Jörn D, Kohorst P, Besdo S, Rücker M, Stiesch M, Borchers L. 2014; Influence of lubricant on screw preload and stresses in a finite element model for a dental implant. J Prosthet Dent. 112:340–8. DOI: 10.1016/j.prosdent.2013.10.016. PMID: 24529658.

35. Inzana JA, Varga P, Windolf M. 2016; Implicit modeling of screw threads for efficient finite element analysis of complex bone-implant systems. J Biomech. 49:1836–44. DOI: 10.1016/j.jbiomech.2016.04.021. PMID: 27157243.

36. Hsu ML, Chen FC, Kao HC, Cheng CK. 2007; Influence of off-axis loading of an anterior maxillary implant: a 3-dimensional finite element analysis. Int J Oral Maxillofac Implants. 22:301–9. DOI: 10.1016/S0021-9290(06)85337-6. PMID: 17465356.

37. Chang CL, Chen CS, Huang CH, Hsu ML. 2012; Finite element analysis of the dental implant using a topology optimization method. Med Eng Phys. 34:999–1008. DOI: 10.1016/j.medengphy.2012.06.004. PMID: 22770748.

38. Martin WC, Woody RD, Miller BH, Miller AW. 2011; Implant abutment screw rotations and preloads for four different screw materials and surfaces. J Prosthet Dent. 86:24–32. DOI: 10.1067/mpr.2001.116230. PMID: 11458261.

39. Lang LA, Kang B, Wang RF, Lang BR. 2003; Finite element analysis to determine implant preload. J Prosthet Dent. 90:539–46. DOI: 10.1016/j.prosdent.2003.09.012. PMID: 14668754.