Korean J Orthod.  2018 Jan;48(1):3-10. 10.4041/kjod.2018.48.1.3.

Prediction of optimal bending angles of a running loop to achieve bodily protraction of a molar using the finite element method

• Ryu WK
• Park JH
• Tai K
• Kojima Y
• Lee Y
• Chae JM

• KMID: 2441436
• DOI: http://doi.org/10.4041/kjod.2018.48.1.3

Abstract

OBJECTIVE
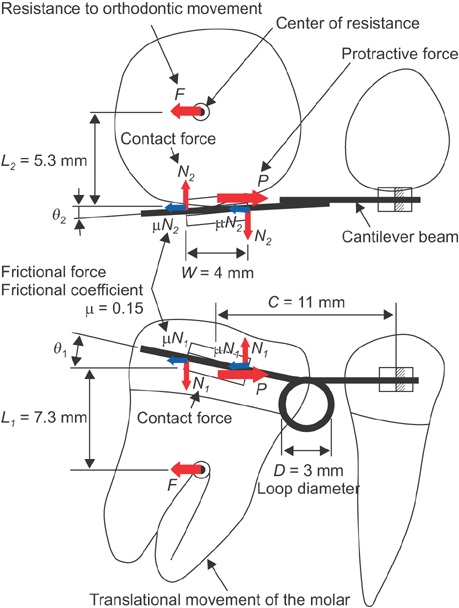
The purpose of this study was to predict the optimal bending angles of a running loop for bodily protraction of the mandibular first molars and to clarify the mechanics of molar tipping and rotation.
METHODS
A three-dimensional finite element model was developed for predicting tooth movement, and a mechanical model based on the beam theory was constructed for clarifying force systems.
RESULTS
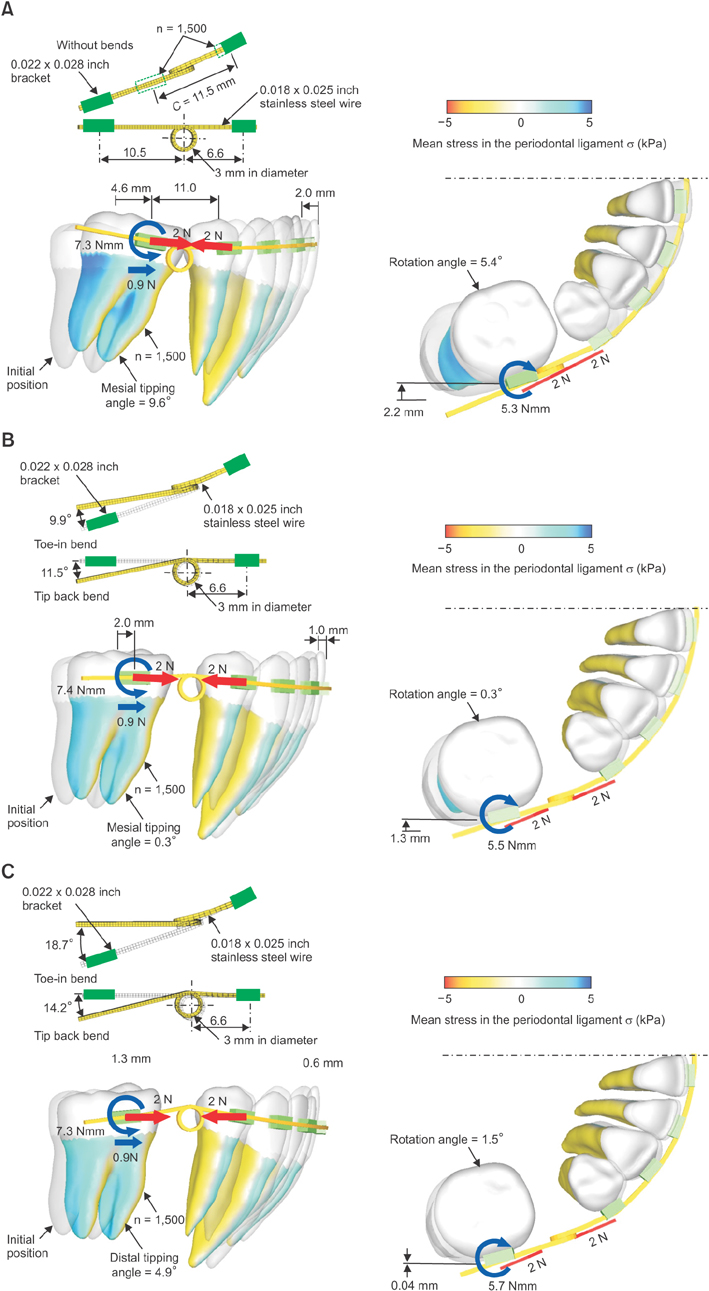
When a running loop without bends was used, the molar tipped mesially by 9.6° and rotated counterclockwise by 5.4°. These angles were almost similar to those predicted by the beam theory. When the amount of tip-back and toe-in angles were 11.5° and 9.9°, respectively, bodily movement of the molar was achieved. When the bend angles were increased to 14.2° and 18.7°, the molar tipped distally by 4.9° and rotated clockwise by 1.5°.
CONCLUSIONS
Bodily movement of a mandibular first molar was achieved during protraction by controlling the tip-back and toe-in angles with the use of a running loop. The beam theory was effective for understanding the mechanics of molar tipping and rotation, as well as for predicting the optimal bending angles.

Keyword

Finite element method; Molar protraction; Running loop; Tip-back angle

MeSH Terms

Decompression Sickness
Mechanics
Methods*
Molar*
Running*
Tooth Movement

Figure

• 

  Figure 1 Finite element model for simulating orthodontic tooth movement.

• 

  Figure 2 Forces acting on the molar under translational movement.

• 

  Figure 3 Effect of bending angles of the running loop on the tooth movement pattern. A, Without bends; B, tip-back angle (11.5°), toe-in angle (9.9°); C, tip-back angle (14.2°), toe-in angle (18.7°).

• 

  Figure 4 Tooth movement produced by the running loop used in clinical treatment.

Reference

1. Proffit WR. Forty-year review of extraction frequencies at a university orthodontic clinic. Angle Orthod. 1994; 64:407–414.

2. Schoppe RJ. An Analysis of second premolar extraction procedures. Angle Orthod. 1964; 34:292–302.

3. Brandt S, Safirstein GR. Different extractions for different malocclusions. Am J Orthod. 1975; 68:15–41.

4. Na JY, Kim TW, Yang WS. Orthodontic treatment with upper first and lower second premolars extracted. Korean J Orthod. 1996; 26:113–124.

5. Schumacher HA, Bourauel C, Drescher D. Analysis of forces and moments in arch guided molar protraction using Class I and Class II elastics. An invitro study. J Orofac Orthop. 1996; 57:4–14.

6. Romeo DA, Burstone CJ. Tip-back mechanics. Am J Orthod. 1977; 72:414–421.

7. Kusy RP. Influence of force systems on archwire-bracket combinations. Am J Orthod Dentofacial Orthop. 2005; 127:333–342.

8. Siatkowski RE. Force system analysis of V-bend sliding mechanics. J Clin Orthod. 1994; 28:539–546.

9. Chae J, Kim S. Running loop in unusual molar extraction treatment. Am J Orthod Dentofacial Orthop. 2007; 132:528–539.

10. Technique clinic. The shoehorn technique. J Clin Orthod. 1970; 4:228–229.

11. Peretta R, Segù M. Cherry loop: a new loop to move the mandibular molar mesially. Prog Orthod. 2001; 2:24–29.

12. Kojima Y, Kawamura J, Fukui H. Finite element analysis of the effect of force directions on tooth movement in extraction space closure with miniscrew sliding mechanics. Am J Orthod Dentofacial Orthop. 2012; 142:501–508.

13. Kojima Y, Fukui H. Numerical simulations of canine retraction with T-loop springs based on the updated moment-to-force ratio. Eur J Orthod. 2012; 34:10–18.

14. Cho SM, Choi SH, Sung SJ, Yu HS, Hwang CJ. The effects of alveolar bone loss and miniscrew position on initial tooth displacement during intrusion of the maxillary anterior teeth: Finite element analysis. Korean J Orthod. 2016; 46:310–322.

15. Kusy RP, Whitley JQ, Prewitt MJ. Comparison of the frictional coefficients for selected archwire-bracket slot combinations in the dry and wet states. Angle Orthod. 1991; 61:293–302.

16. Timoshenko SP, Young DH. Element of strength of materials. 5th ed. Princeton, NJ: Van Nostrand Maruzen;1968.

17. Soenen PL, Dermaut LR, Verbeeck RM. Initial tooth displacement in vivo as a predictor of long-term displacement. Eur J Orthod. 1999; 21:405–411.

18. Mühlemann HR. 10 years of tooth-mobility measurements. J Periodont. 1960; 31:110–122.