J Korean Assoc Oral Maxillofac Surg.  2018 Apr;44(2):59-65. 10.5125/jkaoms.2018.44.2.59.

Three-dimensional optimization and sensitivity analysis of dental implant thread parameters using finite element analysis

• Geramizadeh M
• Katoozian
• Amid R
• Kadkhodazadeh M

• KMID: 2410581
• DOI: http://doi.org/10.5125/jkaoms.2018.44.2.59

Abstract

OBJECTIVES
This study aimed to optimize the thread depth and pitch of a recently designed dental implant to provide uniform stress distribution by means of a response surface optimization method available in finite element (FE) software. The sensitivity of simulation to different mechanical parameters was also evaluated.
MATERIALS AND METHODS
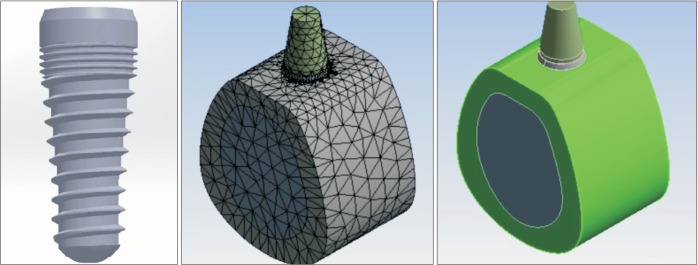
A three-dimensional model of a tapered dental implant with micro-threads in the upper area and V-shaped threads in the rest of the body was modeled and analyzed using finite element analysis (FEA). An axial load of 100 N was applied to the top of the implants. The model was optimized for thread depth and pitch to determine the optimal stress distribution. In this analysis, micro-threads had 0.25 to 0.3 mm depth and 0.27 to 0.33 mm pitch, and V-shaped threads had 0.405 to 0.495 mm depth and 0.66 to 0.8 mm pitch.
RESULTS
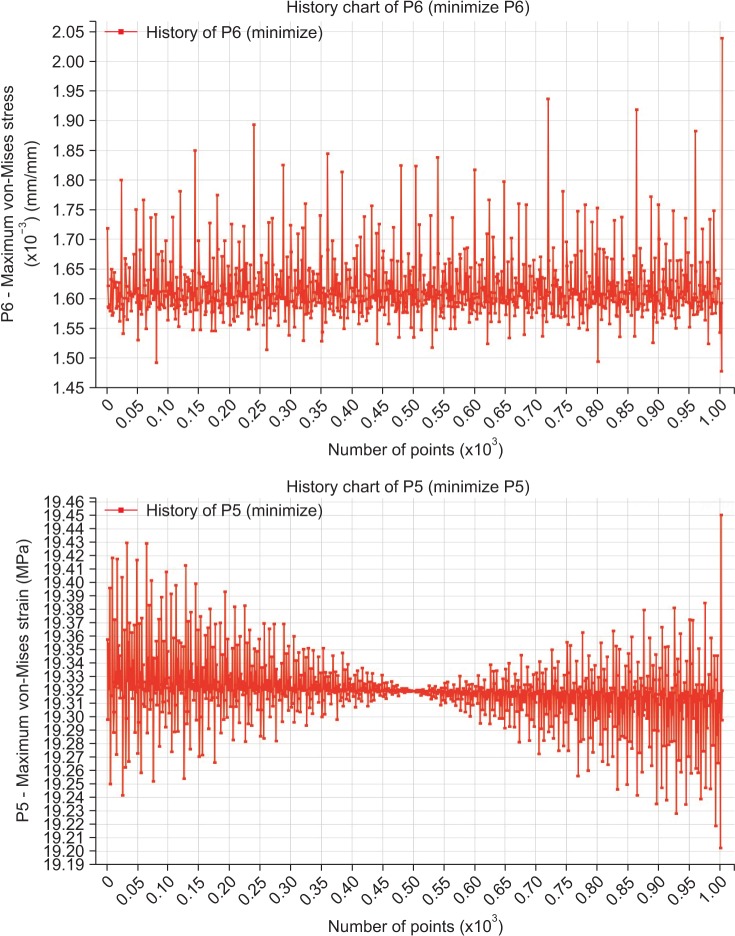
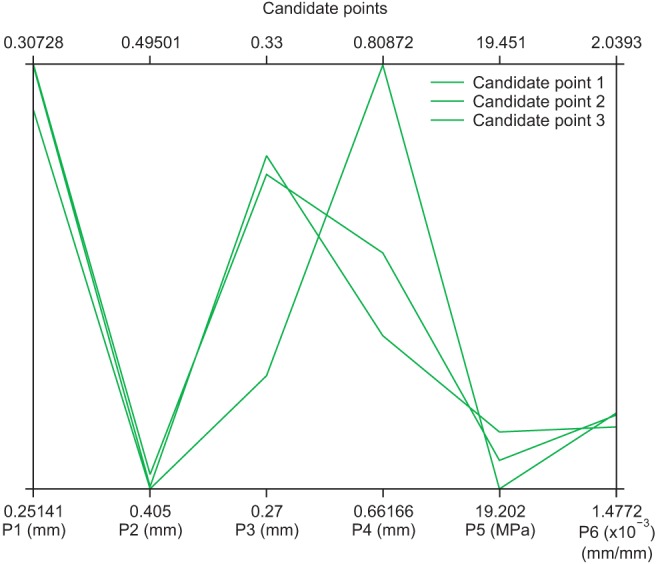
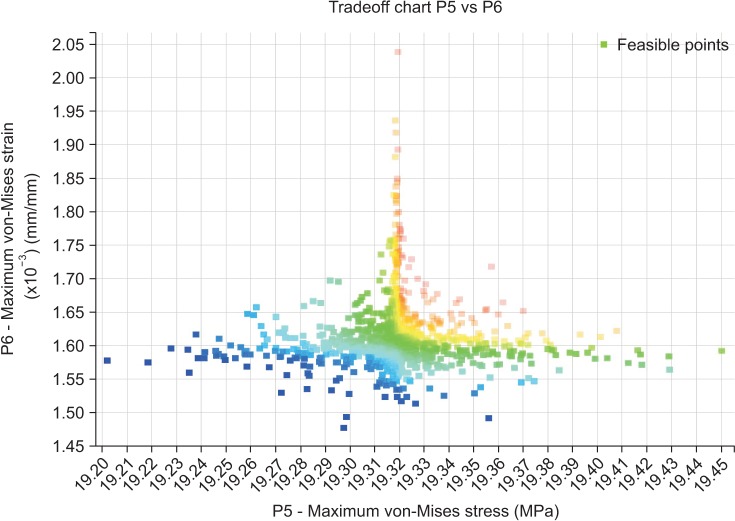
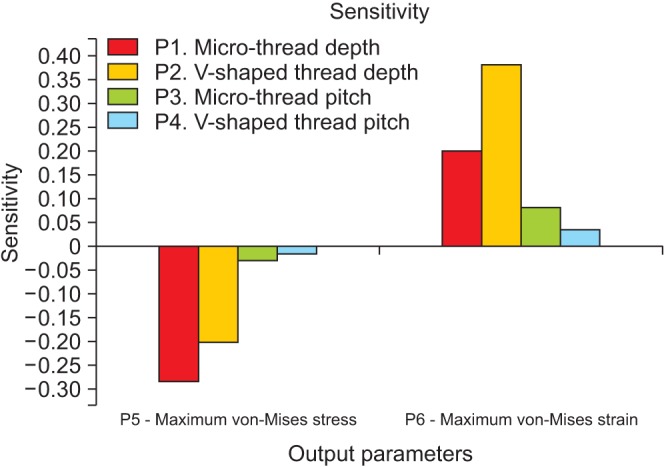
The optimized depth and pitch were 0.307 and 0.286 mm for micro-threads and 0.405 and 0.808 mm for V-shaped threads, respectively. In this design, the most effective parameters on stress distribution were the depth and pitch of the micro-threads based on sensitivity analysis results.
CONCLUSION
Based on the results of this study, the optimal implant design has micro-threads with 0.307 and 0.286 mm depth and pitch, respectively, in the upper area and V-shaped threads with 0.405 and 0.808 mm depth and pitch in the rest of the body. These results indicate that micro-thread parameters have a greater effect on stress and strain values.

Keyword

Dental implants; Thread design; Optimization; Biomechanics; Finite element

MeSH Terms

Clothing
Dental Implants*
Finite Element Analysis*
Methods
Dental Implants

Figure

• 

  Fig. 1 Implant model and the whole model.

• 

  Fig. 2 Iterations of solving the problem to find the perfect candidates to optimize the chosen parameters.

• 

  Fig. 3 Three candidate points for output results (P1: microthread depth, P2: V-shaped thread depth, P3: micro-thread pitch, P4: V-shaped thread pitch, P5: maximum von-Mises stress, P6: maximum von-Mises strain).

• 

  Fig. 4 Consideration of stress and strain quantities to find the best points to minimize both (green zone).

• 

  Fig. 5 Sensitivity analysis of maximum stress and strain with respect to the four input parameters.

Reference

1. Gosavi SP, Dhatrak PN, Narkar KM. Optimisation of dental implant. Int Eng Res J. 2015; 3:4319–4323.

2. Brunski JB. Biomaterials and biomechanics in dental implant design. Int J Oral Maxillofac Implants. 1988; 3:85–97. PMID: 3075195.

3. Mahajan S, Patil R. Application of finite element analysis to optimizing dental implant. Int Res J Eng Technol. 2016; 3:850–856.

4. Kong L, Zhao Y, Hu K, Li D, Zhou H, Wu Z, et al. Selection of the implant thread pitch for optimal biomechanical properties: a three-dimensional finite element analysis. Adv Eng Softw. 2009; 40:474–478.

5. Petrie CS, Williams JL. Shape optimization of dental implant designs under oblique loading using the p-version finite element method. J Mech Med Biol. 2002; 3:339.

6. Shi L, Li H, Fok AS, Ucer C, Devlin H, Horner K. Shape optimization of dental implants. Int J Oral Maxillofac Implants. 2007; 22:911–920. PMID: 18271372.

7. Chang CL, Chen CS, Huang CH, Hsu ML. Finite element analysis of the dental implant using a topology optimization method. Med Eng Phys. 2012; 34:999–1008. PMID: 22770748.

8. Shen S, Sun Y, Zhang C, Yang Y, Li Z, Cai X, et al. Bivariate optimization of orthodontic mini-implant thread height and pitch. Int J Comput Assist Radiol Surg. 2015; 10:109–116. PMID: 25159301.

9. Hasan I, Rahimi A, Keilig L, Brinkmann KT, Bourauel C. Computational simulation of internal bone remodelling around dental implants: a sensitivity analysis. Comput Methods Biomech Biomed Engin. 2012; 15:807–814. PMID: 21442491.

10. Geramizadeh M, Katoozian H, Amir R, Kadkhodazadeh M. Static, dynamic, and fatigue finite element analysis of dental implants with different thread designs. J Long Term Eff Med Implants. 2016; 26:347–355. PMID: 29199621.

11. Geramizadeh M, Katoozian H, Amid R, Kadkhodazadeh M. Finite element analysis of dental implants with and without microthreads under static and dynamic loading. J Long Term Eff Med Implants. 2017; 27:25–35. PMID: 29604947.

12. Seong WJ, Kim UK, Swift JQ, Heo Y, Hodges JS, Ko CC. Elastic properties and apparent density of human edentulous maxilla and mandible. Int J Oral Maxillofac Surg. 2009; 38:1088–1093. PMID: 19647417.

13. Tortorelli DA, Michaleris P. Design sensitivity analysis: overview and review. Inverse Probl Eng. 1994; 1:71–105.

14. Kayabaşı O, Yüzbasıoğlu E, Erzincanlı F. Static, dynamic and fatigue behaviors of dental implant using finite element method. Adv Eng Softw. 2006; 37:649–658.