Korean J Physiol Pharmacol.  2011 Dec;15(6):371-382. 10.4196/kjpp.2011.15.6.371.

A Computational Model of the Temperature-dependent Changes in Firing Patterns in Aplysia Neurons

• Hyun NG
• Hyun KH
• Hyun KB
• Han JH
• Lee K
• Kaang BK

• KMID: 2285424
• DOI: http://doi.org/10.4196/kjpp.2011.15.6.371

Abstract

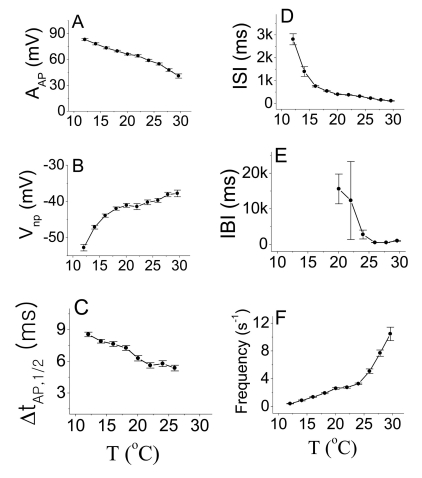
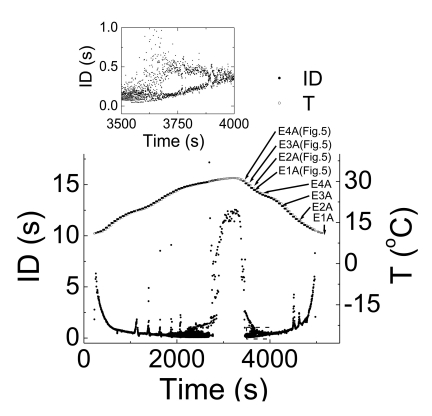
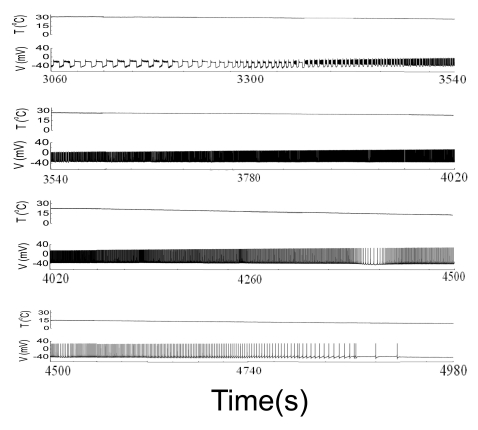
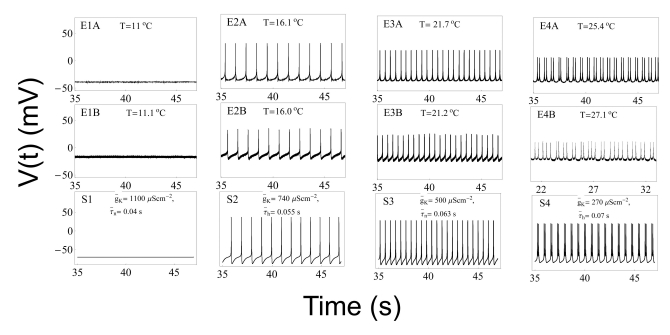
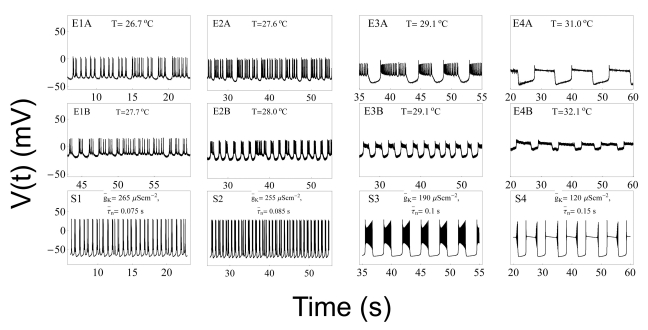
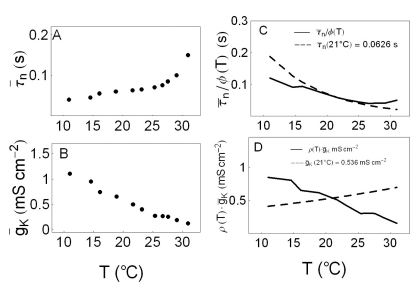
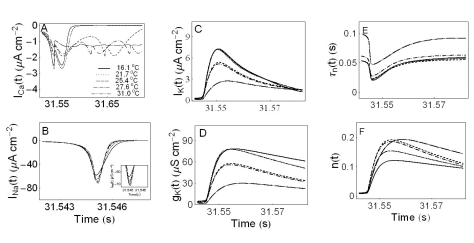
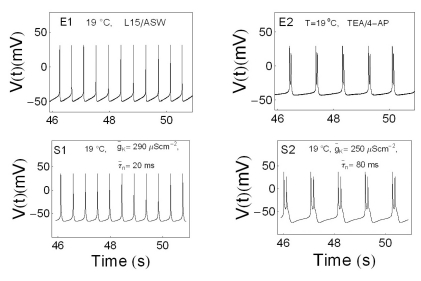
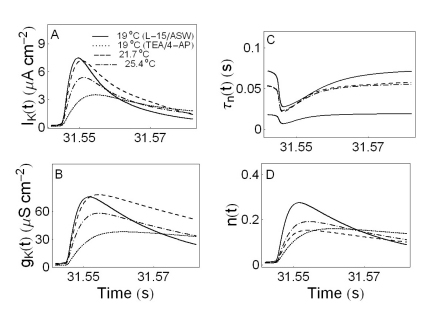
We performed experiments using Aplysia neurons to identify the mechanism underlying the changes in the firing patterns in response to temperature changes. When the temperature was gradually increased from 11degrees C to 31degrees C the firing patterns changed sequentially from the silent state to beating, doublets, beating-chaos, bursting-chaos, square-wave bursting, and bursting-oscillation patterns. When the temperature was decreased over the same temperature range, these sequential changes in the firing patterns reappeared in reverse order. To simulate this entire range of spiking patterns we modified nonlinear differential equations that Chay and Lee made using temperature-dependent scaling factors. To refine the equations, we also analyzed the spike pattern changes in the presence of potassium channel blockers. Based on the solutions of these equations and potassium channel blocker experiments, we found that, as temperature increases, the maximum value of the potassium channel relaxation time constant, taun(t) increases, but the maximum value of the probabilities of openings for activation of the potassium channels, n(t) decreases. Accordingly, the voltage-dependent potassium current is likely to play a leading role in the temperature-dependent changes in the firing patterns in Aplysia neurons.

Keyword

Aplysia; Bursting; Doublet; Temperature-dependent scaling factor; Computer simulation

MeSH Terms

Aplysia
Computer Simulation
Fires
Neurons
Potassium
Potassium Channel Blockers
Potassium Channels
Relaxation
Potassium
Potassium Channel Blockers
Potassium Channels

Figure

• 

  Fig. 1 Average values of six AP parameters with error bars. AAP, ΔtAP, 1/2, ISI, and IBI displayed in panels A, C, D, and E, respectively, decreased as temperature increased. |Vnp| and Frequency displayed in panels B and F, respectively, increased as temperature increased.

• 

  Fig. 2 Temperature and ID as a function of time. Data acquired from one temperature cycle in Experiment A are plotted. The near symmetry of the graph is taken to mean that the time-dependence of the data to be analyzed is reproducible. The small upper box displays a magnified view from 3,500 s to 4,000 s. The symbols E1A to E4A (Fig. 5), written in the large bottom box correspond to the time series displayed in each panel in Fig. 4E1A to Fig. 5E4A. Sinusoidal bursting with very long burst duration and short IBI is shown by the sign looked like "∧" in the bottom trace.

• 

  Fig. 3 The upper and lower traces represent temperature and membrane potential, respectively. When the temperature was decreased from 31℃ to 11℃, the seven firing patterns of Aplysia neurons changed sequentially: bursting-oscillation, square-wave bursting, bursting-chaos, beating-chaos, doublets, beating, and silent.

• 

  Fig. 4 Comparison of experimental results with results from computer simulations. Panels E1A~E4A display data from Experiment A. Panels E1B~E4B display data from Experiment B. The relevant temperatures are shown at the top of each box. Panels S1~S4 display values calculated from equations (1) to (4) using parameters from the type 1 model at the temperatures shown in panels E1A~E4A, respectively. The variables g̅K and τ̅n nused in the simulations are shown at the top of the boxes in the bottom panel of each set of three panels. Panels E1A, E1B, and S1 display silent pattern. Panels E2A, E3A, E2B, E3B, S2 and S3 display beating pattern. Panels E4A, E4B, and S4 display doublet pattern.

• 

  Fig. 5 Comparison of experimental results with results from computer simulations. Panels E1A~E4A display data from Experiment A. Panels E1B~E4B display data from Experiment B. The relevant temperatures are shown at the top of each box. Panels S1~S4 display values calculated from equations (1) to (4) using parameters from the type 1 model at the temperatures shown in panels E1A~E4A, respectively. The variables g̅K and τ̅n used in the simulations are shown at the top of the boxes in the bottom panel of each set of three panels. Panels E1A, E1B, and S1 display beating chaos. Panels E2A, E2B, and S2 display bursting chaos. Panels E3A, E3B, and S3 display square-wave bursting. Panels E4A, E4B, and S4 display bursting-oscillation.

• 

  Fig. 6 Simulation variables. Panel A display the variation in τ̅n with respect to temperature. Panel B displays the variation in g̅K with respect to temperature. Panel C displays τ̅n/φ(T). In this panel the dotted line displays the value of τ̅n/φ(T) when τ̅n is a constant value at reference temperature 21℃. The solid line in panel C displays τ̅n/φ(T) with τ̅n as a variable represented in panel A at the corresponding temperatures. At low (high) temperatures the value of τ̅n/φ(T) is smaller (larger) than the expected value, which is shown as a dotted line. Panel D displays ρ(T)·g̅K. In this panel the dotted line displays the value of ρ(T)·g̅K when g̅K is a constant value at reference temperature of 21℃. The solid line in this panel displays the value of ρ(T)·g̅K with g̅K a variable represented in panel B at the corresponding temperatures. Although the dotted line increase as temperature increase, the solid line decrease.

• 

  Fig. 7 Ionic currents and parameters as a function of time. Panel A, B, and C display ICa(t), INa(t), and IK(t), respectively. The solid, dotted, dashed, dash-dotted, dashed-doubledotted lines in panels from A to F are used to represent the variables as a function of time at temperatures 16.1℃, 21.7℃, 25.4℃, 27.6℃, and 31℃, respectively. Panel D displays gk(t). The potassium channel relaxation time constants τn(t) and the probabilities of openings for activation of the potassium channels n(t) as a function of time are shown in panels E and F, respectively.

• 

  Fig. 8 Comparison of beating and bursting signals influenced or uninfluenced by drugs with simulation results. Panel E1 and E2 represents time series of APs without drug and with the treatment of drugs mixed with 10 mM TEA and 10 mM 4-AP, respectively. Panel S1 and S2 represents the results of computer simulation with modified Chay-Lee model with temperature-like scaling factors.

• 

  Fig. 9 Ionic currents and parameters as a function of time. Panel A and B display IK(t) and gK(t), respectively. The potassium channel relaxation time constants τn(t) and the probabilities of openings for activation of the potassium channels n(t) as a function of time are shown in panels C and D, respectively. The solid, dotted, dashed, and dash-dotted lines in panels from A to D indicate L15/ASW medium control without drugs at 19℃, L15/ASW medium containing 10 mM TEA and 10 mM 4-AP at 19℃, L15/ASW medium at 21.7℃, and L15/ASW medium at 25.4℃, respectively.

Reference

1. Carpenter DO. Temperature effects on pacemaker generation, membrane potential, and critical firing threshold in Aplysia neurons. J Gen Physiol. 1967; 50:1469–1484. PMID: 6034753.

2. Moffett S, Wachtel H. Correlations between temperature effects on behavior in Aplysia and firing patterns of identified neurons. Mar Behav Physiol. 1976; 4:61–74.

3. Carpenter DO, Alving BO. A contribution of an electrogenic Na⁺ pump to membrane potential in Aplysia neurons. J Gen Physiol. 1968; 52:1–21. PMID: 5742832.

4. Fletcher SD, Ram JL. High temperature induces reversible silence in Aplysia R15 bursting pacemaker neuron. Comp Biochem Physiol. 1991; 98A:399–405.

5. Hakozaki S, Matsumoto M, Sasaki K. Temperature-sensitive activation of G-protein regulating the resting membrane conductance of Aplysia neurons. Jpn J Physiol. 1989; 39:115–130. PMID: 2498557.

6. Chay TR. Bursting excitable cell models by a slow Ca²⁺ current. J Theor Biol. 1990; 142:305–315. PMID: 2160027.

7. Chay TR, Lee YS. Bursting, beating, and chaos by two functionally distinct inward current inactivations in excitable cells. Ann N Y Acad Sci. 1990; 591:328–350. PMID: 2165373.

8. Hensel H, Huopaniemi T. Static and dynamic properties of warm fibres in the infraorbital nerve. Pflugers Arch. 1969; 309:1–10. PMID: 5815315.

9. Hensel H, Schäfer K. Static an dynamic activity of cold receptors in cats after long-term exposure to various temperatures. Pflugers Arch. 1982; 392:291–294. PMID: 7070961.

10. Schäfer K, Braun HA, Kürten L. Analysis of cold and warm receptor activity in vampire bats and mice. Pflugers Arch. 1988; 412:188–194. PMID: 3174381.

11. Hensel H. Static and dynamic activity of warm receptors in Boa constrictor. Pflugers Arch. 1975; 353:191–199. PMID: 1168336.

12. Kim YD, Cho MH, Kwon SC. Myoplasmic [Ca²⁺], crossbridge phosphorylation and latch in rabbit bladder smooth muscle. Korean J Physiol Pharmacol. 2011; 15:171–177. PMID: 21860596.

13. Kim KS, Shin DH, Nam JH, Park KS, Zhang YH, Kim WK, Kim SJ. Functional expression of TRPV4 cation channels in human mast cell line (HMC-1). Korean J Physiol Pharmacol. 2010; 14:419–425. PMID: 21311684.

14. Braun HA, Huber MT, Dewald M, Schäfer K, Voigt K. Computer simulations of neuronal signal transduction: the role of nonlinear dynamics and noise. Int J Bifurcation Chaos. 1998; 8:881–889.

15. Finke C, Freund JA, Rosa E Jr, Braun HA, Feudel U. On the role of subthreshold currents in the Huber-Braun cold receptor model. Chaos. 2010; 20:045107. PMID: 21198119.

16. Lim CS, Chung DY, Kaang BK. Partial anatomical and physiological characterization and dissociated cell culture of the nervous system of the marine mollusc Aplysia kurodai. Mol Cells. 1997; 7:399–407. PMID: 9264029.

17. Hyun NG, Hyun KH, Lee K, Kaang BK. Temperature Dependence of Action Potential Parameters in Aplysia Neurons. Neurosignals. 2011; (in press).

18. Hille B. Ion channels of excitable membranes. 2001. 3rd ed. Sunderland Mass: Sinauer;p. 366.

19. Hyun NG. The brain and the mind. 2007. 1st ed. Jeju: Jeju Nat Univ;p. 321–338.

20. Wang LY, Fedchyshyn MJ, Yang YM. Action potential evoked transmitter release in central synapses: insights from the developing calyx of Held. Mol Brain. 2009; 2:36. PMID: 19939269.

21. Volk KA, Matsuda JJ, Shibata EF. A voltage-dependent potassium current in rabbit coronary artery smooth muscle cells. J Physiol. 1991; 439:751–768. PMID: 1910087.

22. Spruce AE, Standen NB, Stanfield PR. The action of external tetraethylammonium ions on unitary delayed rectifier potassium channels of frog skeletal muscle. J Physiol. 1987; 393:467–478. PMID: 2451742.