Yonsei Med J.  2011 Sep;52(5):818-830. 10.3349/ymj.2011.52.5.818.

Limb Angular Deformity Correction Using Dyna-ATC: Surgical Technique, Calculation Method, and Clinical Outcome

• Park H
• Kim HW
• Park HW
• Lee KS

• KMID: 1108076
• DOI: http://doi.org/10.3349/ymj.2011.52.5.818

Abstract

PURPOSE
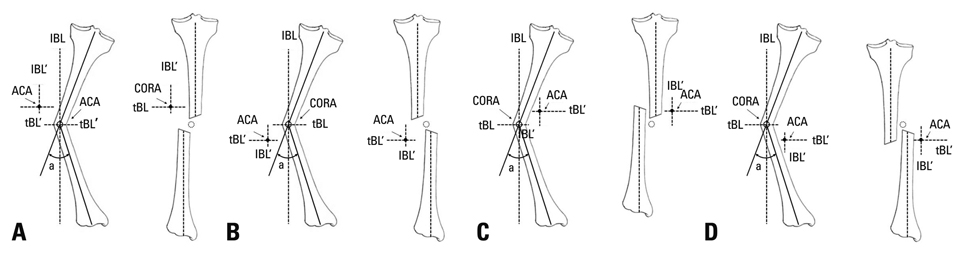
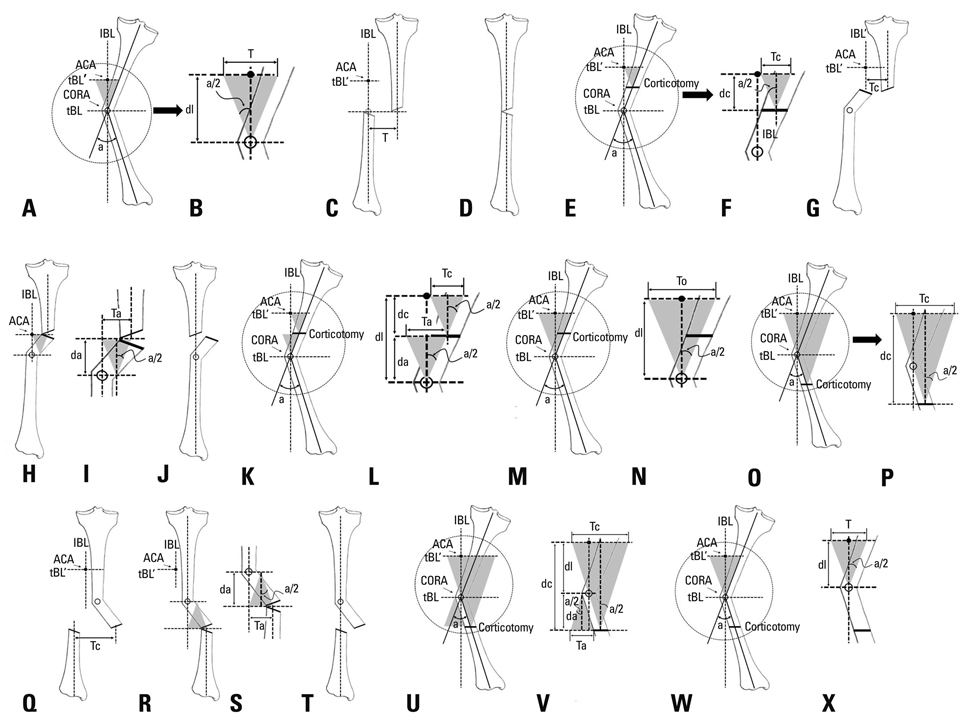
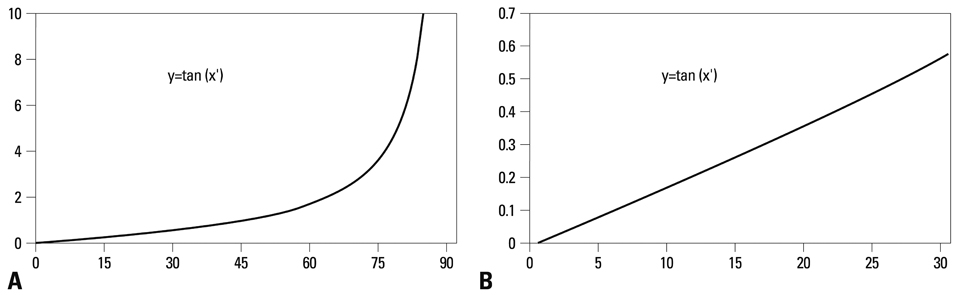
Dyna-ATC is a unilateral external fixator with angulator, lengthener, and translator, which allows for angular correction and compensation of the secondary displacement during angular correction. The purpose of this study is to introduce surgical technique and calculation methods and to evaluate the clinical outcome of angular deformity correction using Dyna-ATC.
MATERIALS AND METHODS
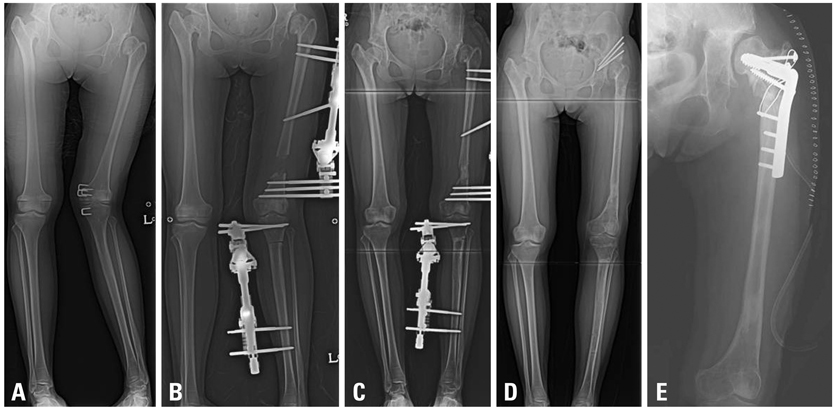
The amounts of secondary displacement were calculated with the distances between axis of correction of angulation, Center of Rotational Angulation, and osteotomy and the amount of angular deformity. The rate of angular correction was determined to distract the corticotomy at 1 mm/day. Clinical and radiographic evaluation was performed on 13 patients who underwent deformity correction using Dyna-ATC. There were 8 proximal tibia vara, 1 tibia valga, 2 varus and 4 valgus deformities on distal femur. One patient underwent pelvic support femoral reconstruction. Concomitant lengthening was combined in all femur cases. Mean age at surgery was 17.5 years (7 to 64).
RESULTS
All but one achieved bony healing and normal alignment with the index procedure. Mean mechanical axis deviation improved from 31.9 mm to 3.0 mm. The average amount of angular correction was 11.0degrees on tibiae and 10.0degrees on femora. The average length gain on femora was 6.4 cm, and the healing index averaged to 1.1 mo/cm. One patient underwent quadricepsplasty and one patient had three augmentation surgeries due to poor new bone formation.
CONCLUSION
We believe that Dyna-ATC is a useful alternative to bulky ring fixators for selective patients with angular deformity less than 30 degrees in the coronal plane around the knee joint.

Keyword

Limb angular deformity; unilateral external fixator; dyna-ATC; calculation method

MeSH Terms

Adolescent
Bone Diseases, Developmental/*surgery
Child
*External Fixators
Female
Femur/abnormalities/surgery
Humans
Leg Length Inequality/surgery
Lower Extremity Deformities, Congenital/*surgery
Male
Middle Aged
Osteochondrosis/congenital/surgery
Osteogenesis, Distraction/*instrumentation/methods/statistics & numerical data
Osteotomy
Tibia/abnormalities/surgery
Treatment Outcome
Young Adult

Figure

• 

  Fig. 1 Dyna-ATC: Standard type (A) and T-type (B).

• 

  Fig. 2 ACA-CORA Rule 1. If the ACA is located on the concave side of angular deformity, secondary lengthening at the corticotomy develops after angular correction (A) and if the ACA is located on the convex side, secondary shortening develops (B). ACA, axis of correction of angulation; lBL, longitudinal bisecting line; CORA, Center of Rotational Angulation; tBL, transverse bisection line; L, amount of secondary lengthening; S, amount of secondary shortening.

• 

  Fig. 3 ACA-CORA Rule 2. If the ACA is not located on the transverse bisection line (tBL) of the CORA, the secondary translation develops after angular correction. The fragment on the opposite side to the ACA moves toward the convex side of the angular deformity. ACA, axis of correction of angulation; lBL, longitudinal bisecting line; CORA, Center of Rotational Angulation.

• 

  Fig. 4 Secondary length change after angular correction when the ACA is not on the CORA (C and G) can be calculated before angular correction (A, B, E, F) and be compensated during angular correction (D and H). To avoid abutment during angular correction, secondary length change to be compensated should be calculated at the convex side of the corticotomy. 1) Secondary lengthening when the ACA is on the convex side of the CORA (A-D). L=2×dt×tan (a/2). 2) Secondary shortening when the ACA is on the convex side of the CORA (E-H). S=2×dt×tan (a/2). L, the amount of lengthening to be compensated; dt, distance from the ACA to the convex side of the corticotomy over the tBL of the CORA; a, the amount of angular deformity to be corrected. S, the amount of shortening to be compensated. ACA, axis of correction of angulation; lBL, longitudinal bisecting line; CORA, Center of Rotational Angulation; tBL, transverse bisection line.

• 

  Fig. 5 Secondary translation after angular deformity when the ACA is not on the CORA (N and X) can be calculated before angular correction and should be compensated during angular correction. If the corticotomy is not performed on the CORA, zigzag deformity develops even after the compensation of the secondary translation (H and R). To avoid this zigzag deformity, additional translation is needed (I and S). The amount of additional translation also can be calculated before angular correction. 1) Secondary translation when the ACA is not on the CORA (A-D). T=2×dl×tan (a/2). 2) Secondary translation when the ACA is not on the CORA and corticotomy is not on the CORA but on the side of the ACA (E-N). The amount of translation at the corticotomy site can be calculated with the amount of the angular deformity to be corrected and the distance between the ACA and the corticotomy over the lBL (F, G, P, Q). However, after the compensation, zigzag deformity still remains (H and R) and additional compensatory translation to the same direction for the realignment of the corticotomy is needed (H and R). The additional translation can be calculated with the amount of angular deformity to be corrected and the distance between the corticotomy and the CORA (I and S). a) Secondary translation at the corticotomy site (E, F and G). Tc=2×dc×tan (a/2) (F). b) Additional translation to be compensated to avoid zigzag deformity (H and I). Ta=2 ×da×tan (a/2) (I). c) Overall translation to be compensated (K-N). If the corticotomy is not on the CORA but on the side of the ACA, additional translation should be compensated to the same direction to that for the corticotomy. To=Tc+Ta=2×dc×tan (a/2)+2×da×tan (a/2)=2×(dc+da)×tan (a/2)=2×dl×tan (a/2) (L and N). 3) Secondary translation when the ACA is not on the CORA and corticotomy is not on the CORA but on the other side of the ACA (O-X). The amount of translation at the corticotomy site and the amount of additional translation to avoid zigzag deformity also can be calculated with the amount of the angular deformity to be corrected and the distances between the ACA and the corticotomy and between the corticotomy and the CORA over the lBL. However, the direction of the compensatory additional translation is the opposite to that for the corticotomy site (Q, R and T). a) Secondary translation at the corticotomy site (O-Q). Tc=2×dc×tan (a/2) (P). b) Additional translation to be compensated to avoid zigzag deformity (R and S). Ta=2×da×tan (a/2) (S). c) Overall translation to be compensated (U-X). If the corticotomy is not on the CORA but on the side of the ACA, additional translation should be compensated to the opposite direction to that for the corticotomy (Q, R and T). To=Tc-Ta=2×dc×tan (a/2)-2×da×tan (a/2)=2×(dc-da)×tan (a/2)=2×dl×tan (a/2) (V and X). 4) Therefore, regardless of the location of the corticotomy, the overall amount of compensatory translation can be calculated with the amount of angular correction and the distance between the ACA and the CORA over the lBL (K-N, U-X). T, the amount of translation to be compensated; dl, distance from the ACA to the CORA over the longitudinal bisection line (lBL) of the CORA; a, the amount of angular deformity to be corrected. Tc, the amount of translation at the corticotomy site; dc, distance from the ACA to the corticotomy over the lBL; Ta, the amount of additional translation to avoid zigzag deformity; da, distance from the corticotomy to the CORA over the lBL; To, the overall amount of translation to be compensated. ACA, axis of correction of angulation; CORA, Center of Rotational Angulation.

• 

  Fig. 6 Correction rate calculation. During angular correction, secondary length change and translation are compensated continuously, therefore, correction rate can be calculated with the amount of displacement on the concave side of the corticotomy (D, G and H). 1) Even in cases which do not require lengthening, the concave side of the corticotomy should be open to correction angular deformity (C). The amount of distraction can be calculated with the distance between the convex and concave side of the corticotomy and the amount of angular correction. l=2×dcv×tan (a/2) (D). 2) If the corticotomy are on tBL of the CORA (E), as shown in Fig 5. additional translation is needed for exact realignment (F and G). In this case, although exact realignment is achieved, translation of the corticotomy site still remains after correction (G and H). This translation can be calculated with the distance between the corticotomy and the CORA over the lBL. t=2×da×tan (a/2) (F). 3) Overall displacement on the concave side of the corticotomy is D=(l2+t2)1/2(H). 4) Daily amount of angular correction is the angle that make D=1 mm. D=(l2 + t2)1/2=1. D=[{2×dcv×tan (φ/2)}2+{2×da×tan (φ/2)}2]1/2=1. D=22×dcv2×{tan (φ/2)}2+22×da2×{tan (φ/2)}2=1. D=22×(dcv2+da2)×{tan (φ/2)}2=1. {tan (φ/2)}2=(dcv2+da2)-1×2-2. tan (φ/2)=(dcv2+da2)-1/2×2-1. φ=2×cot {(dcv2+da2)-1/2×2-1}. l, the amount of lengthening on the concave side of the corticotomy; dcv, distance from the concave to the convex side of the corticotomy; a, the amount of angular deformity to be corrected; D, Overall displacement on the concave side of the corticotomy in mm; t, the amount of additional translation at the corticotomy site; da, distance from the corticotomy to the CORA over the lBL; φ, the amount of daily angular correction; cot, cotangent. tBL, transverse bisection line; CORA, Center of Rotational Angulation; lBL, longitudinal bisecting line.

• 

  Fig. 7 Tangent function curve. Generally the value of tangent angle increases exponentially (A), however, the curve is relatively straight less than 30 degrees (B).

• 

  Fig. 8 Case 1. A 7-year-old boy with Blount's disease. Despite previous treatments, proximal tibia vara on left side did not improve (A). Intraoperative valgus stress arthrogram showed mild dye pooling on medial side (B). Gradual angular correction with application of T-type Dyna-ATC was planned. First, proximal posterior screw was inserted parallel to the proximal tibial joint orientation line on coronal plane and on the proximally extended posterior cortical line of diaphysis in sagittal plane using cannulated drilling over the guide-wire technique (D and G). Then, distal screws were inserted (F and G). The proximal anterior screw was placed with about 5 degrees of convergent angle (C and G). Oblique type osteotomy was performed below the tibial tuberosity (E and G). Secondary deformities and the rate of angular correction were calculated with immediate postoperative radiographs (H). The ACA was located on the concave side of the angular deformity, therefore, fixator should be lengthened during angular correction to compensate secondary shortening. The amount of secondary shortening to be compensated during angular correction is S=2×dt (98 mm)×tan (a/2=26/2)=45.3 mm. The ACA was not on tBL of the CORA but distal to the CORA, therefore, the proximal tibia (the opposite fragment) would translate laterally (to the convex side of the deformity). Proximal tibia should be translated medially to compensate secondary translation during angular correction. The amount of secondary translation to be compensated was T=2×dl (59 mm)×tan (a/2=26/2)=27.2 mm. The rate of angular correction was calculated with the amount of secondary translation on the concave side of the corticotomy (I). The amount of daily angular correction was φ=2×cot [{dcv (25 mm)2+da (13 mm)2}-1/2×2-1]=2.03°. Therefore, the rate of angular correction is 2 and total duration for angular correction was a/φ=26°/(2°/day)=13 days. Daily amount of compensatory lengthening was S=2×dt (98 mm)×tan (φ/2=2/2)=3.42 mm and the daily amount of compensatory translation was T=2×dl (59 mm)×tan (φ/2=2/2)=2.05 mm. After 5 days of latency period, 5 mm of pre-lengthening was performed to avoid impingement of convex side (J). Angular correction was performed for 13 days with the rate of 2°/day. The rate of compensatory lengthening was 3.5 mm/day and the rate of compensatory translation was 2 mm/day. 13 days later, angular correction was achieved (K and L). The fixator was removed 2 months later and the teleradiograph taken at postoperative 3.5 month showed successful realignment (M). ACA, axis of correction of angulation; tBL, transverse bisection line; CORA, Center of Rotational Angulation.

• 

  Fig. 9 Case 2. A 15-year-old girl with bilateral DDH. Despite several surgeries, the patient suffered genu valgum with shortening and hip subluxation on the left side (A). Gradual angular correction and lengthening on the femur and acute correction with shortening on the tibia were performed with Dyna-ATCs (B and C). At the time of removal of fixators, Chiari osteotomy was performed (D) and five months later, neck lengthening osteotomy with greater trochanter transfer was added for hip reconstruction (E).

Reference

1. Gilbody J, Thomas G, Ho K. Acute versus gradual correction of idiopathic tibia vara in children: a systematic review. J Pediatr Orthop. 2009. 29:110–114.

2. Feldman DS, Madan SS, Ruchelsman DE, Sala DA, Lehman WB. Accuracy of correction of tibia vara: acute versus gradual correction. J Pediatr Orthop. 2006. 26:794–798.

3. Kamegaya M, Shinohara Y, Shinada Y. Limb lengthening and correction of angulation deformity: immediate correction by using a unilateral fixator. J Pediatr Orthop. 1996. 16:477–479.

4. Noonan KJ, Price CT, Sproul JT, Bright RW. Acute correction and distraction osteogenesis for the malaligned and shortened lower extremity. J Pediatr Orthop. 1998. 18:178–186.

5. Behrens F. General theory and principles of external fixation. Clin Orthop Relat Res. 1989. 15–23.

6. Herbert AJ, Herzenberg JE, Paley D. A review for pediatricians on limb lengthening and the Ilizarov method. Curr Opin Pediatr. 1995. 7:98–105.

7. Noonan KJ, Leyes M, Forriol F, Cañadell J. Distraction osteogenesis of the lower extremity with use of monolateral external fixation. A study of two hundred and sixty-one femora and tibiae. J Bone Joint Surg Am. 1998. 80:793–806.

8. Kim YH, Inoue N, Chao EY. Kinematic simulation of fracture reduction and bone deformity correction under unilateral external fixation. J Biomech. 2002. 35:1047–1058.

9. Birch JG, Samchukov ML. Use of the Ilizarov method to correct lower limb deformities in children and adolescents. J Am Acad Orthop Surg. 2004. 12:144–154.

10. Tsuchiya H, Uehara K, Abdel-Wanis ME, Sakurakichi K, Kabata T, Tomita K. Deformity correction followed by lengthening with the Ilizarov method. Clin Orthop Relat Res. 2002. 176–183.

11. Coogan PG, Fox JA, Fitch RD. Treatment of adolescent Blount disease with the circular external fixation device and distraction osteogenesis. J Pediatr Orthop. 1996. 16:450–454.

12. McCarthy JJ, Ranade A, Davidson RS. Pediatric deformity correction using a multiaxial correction fixator. Clin Orthop Relat Res. 2008. 466:3011–3017.

13. McLawhorn AS, Sherman SL, Blyakher A, Widmann RF. Humeral lengthening and deformity correction with the multiaxial correction system. J Pediatr Orthop B. 2011. 20:111–116.

14. Teruhisa Y, Hiroyuki T, Keisuke S, Tamon K, Katsuro T. Gradual correction of limb deformity using the Heidelberg external fixator. Nihonsougaikoteikenkyukaishi. J Jpn Soc Extern Fixat. 2003. 14:47–51.

15. Price CT, Scott DS, Greenberg DA. Dynamic axial external fixation in the surgical treatment of tibia vara. J Pediatr Orthop. 1995. 15:236–243.

16. Stanitski DF, Srivastava P, Stanitski CL. Correction of proximal tibial deformities in adolescents with the T-Garches external fixator. J Pediatr Orthop. 1998. 18:512–517.

17. Paley D, Tetsworth K. Mechanical axis deviation of the lower limbs. Preoperative planning of uniapical angular deformities of the tibia or femur. Clin Orthop Relat Res. 1992. 48–64.

18. Paley D, Herzenberg JE, Tetsworth K, McKie J, Bhave A. Deformity planning for frontal and sagittal plane corrective osteotomies. Orthop Clin North Am. 1994. 25:425–465.

19. Paley D. Problems, obstacles, and complications of limb lengthening by the Ilizarov technique. Clin Orthop Relat Res. 1990. 81–104.

20. Gladbach B, Heijens E, Pfeil J, Paley D. Calculation and correction of secondary translation deformities and secondary length deformities. Orthopedics. 2004. 27:760–766.

21. Paley D. Extensive limb lengthening. Baltimore Method. In : 18th Annual Baltimore limb deformity course; 2008, Aug 30; Baltimore, MD.

22. Fadel M, Hosny G. The Taylor spatial frame for deformity correction in the lower limbs. Int Orthop. 2005. 29:125–129.

23. Feldman DS, Madan SS, Koval KJ, van Bosse HJ, Bazzi J, Lehman WB. Correction of tibia vara with six-axis deformity analysis and the Taylor Spatial Frame. J Pediatr Orthop. 2003. 23:387–391.