Prog Med Phys.  2022 Dec;33(4):129-135. 10.14316/pmp.2022.33.4.129.

Dead Layer Thickness and Geometry Optimization of HPGe Detector Based on Monte Carlo Simulation

• Yu S
• Kwon NH
• Jang YJ
• Lee B
• Yu J
• Kim DW
• Cho GS
• Kim KB
• Kim GB
• Baek CH
• Choi SH

• KMID: 2537881
• DOI: http://doi.org/10.14316/pmp.2022.33.4.129

Abstract

Purpose
A full-energy-peak (FEP) efficiency correction is required through a Monte Carlo simulation for accurate radioactivity measurement, considering the geometrical characteristics of the detector and the sample. However, a relative deviation (RD) occurs between the measurement and calculation efficiencies when modeling using the data provided by the manufacturers due to the randomly generated dead layer. This study aims to optimize the structure of the detector by determining the dead layer thickness based on Monte Carlo simulation.
Methods
The high-purity germanium (HPGe) detector used in this study was a coaxial p-type GC2518 model, and a certified reference material (CRM) was used to measure the FEP efficiency. Using the MC N-Particle Transport Code (MCNP) code, the FEP efficiency was calculated by increasing the thickness of the outer and inner dead layer in proportion to the thickness of the electrode.
Results
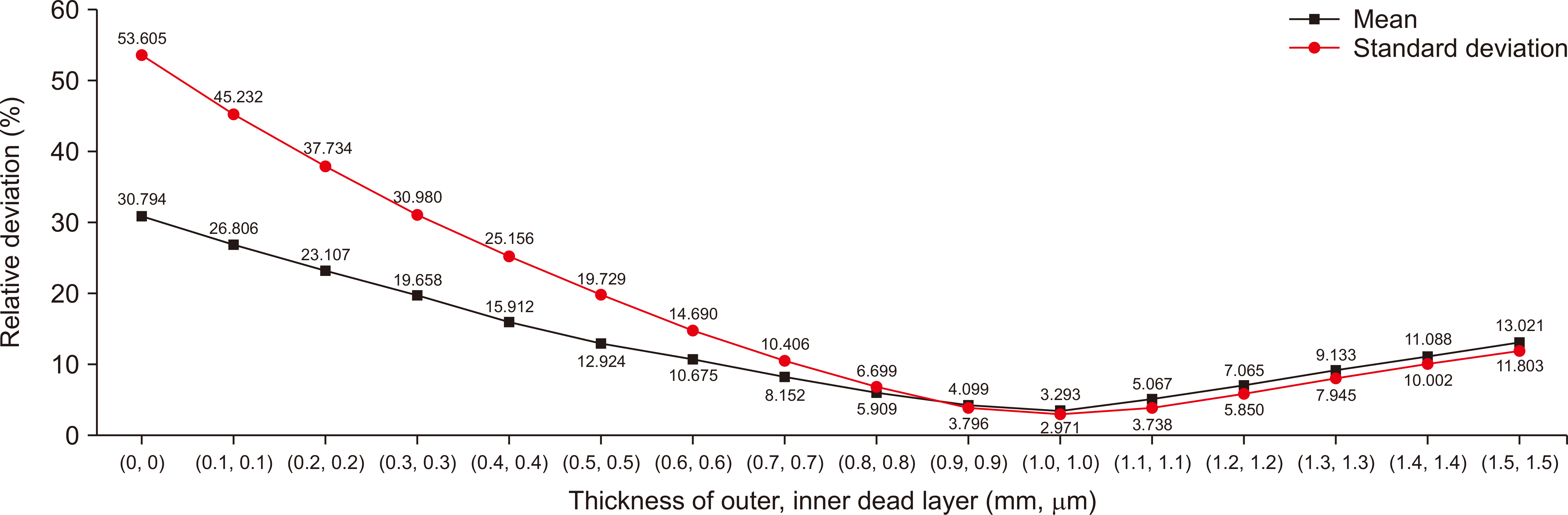
As the thickness of the outer and inner dead layer increased by 0.1 mm and 0.1 µm, the efficiency difference decreased by 2.43% on average up to 1.0 mm and 1.0 µm and increased by 1.86% thereafter. Therefore, the structure of the detector was optimized by determining 1.0 mm and 1.0 µm as thickness of the dead layer.
Conclusions
The effect of the dead layer on the FEP efficiency was evaluated, and an excellent agreement between the measured and calculated efficiencies was confirmed with RDs of less than 4%. It suggests that the optimized HPGe detector can be used to measure the accurate radioactivity using in dismantling and disposing medical linear accelerators.

Keyword

HPGe detector; Dead layer; Monte Carlo simulation; Full-energy-peak efficiency

Figure

• 

  Fig. 1 Internal structure (a) and section of the high-purity germanium (HPGe) detector in the MC N-Particle Transport (MCNP) code (b). CRM, certified reference material.

• 

  Fig. 2 Energy and full width half maximum (FWHM) obtained by gamma-ray spectroscopy.

• 

  Fig. 3 Relative difference between the measured and calculated values according to the dead layer thickness.

Reference

References

1. Alhazmi A, Gianoli C, Neppl S, Martins J, Veloza S, Podesta M, et al. 2018; A novel approach to EPID-based 3D volumetric dosimetry for IMRT and VMAT QA. Phys Med Biol. 63:115002. DOI: 10.1088/1361-6560/aac1a6. PMID: 29714714.

2. Huh HD, Kim S. 2020; History of radiation therapy technology. Prog Med Phys. 31:124–134. DOI: 10.14316/pmp.2020.31.3.124.

3. Farhood B, Ghorbani M, Abdi Goushbolagh N, Najafi M, Geraily G. 2020; Different methods of measuring neutron dose/fluence generated during radiation therapy with megavoltage beams. Health Phys. 118:65–74. DOI: 10.1097/HP.0000000000001130. PMID: 31764421.

4. Israngkul-Na-Ayuthaya I, Suriyapee S, Pengvanich P. 2015; Evaluation of equivalent dose from neutrons and activation products from a 15-MV X-ray LINAC. J Radiat Res. 56:919–926. DOI: 10.1093/jrr/rrv045. PMID: 26265661. PMCID: PMC4628218.

5. Trang LTN, Chuong HD, Thanh TT. 2021; Optimization of p-type HPGe detector model using Monte Carlo simulation. J Radioanal Nucl Chem. 327:287–297. DOI: 10.1007/s10967-020-07473-2.

6. Kaya S, Çelik N, Bayram T. 2022; Effect of front, lateral and back dead layer thicknesses of a HPGe detector on full energy peak efficiency. Nucl Inst Methods Phys Res. 1029:166401. DOI: 10.1016/j.nima.2022.166401.

7. Novotny SJ, To D. 2015; Characterization of a high-purity germanium (HPGe) detector through Monte Carlo simulation and nonlinear least squares estimation. J Radioanal Nucl Chem. 304:751–761. DOI: 10.1007/s10967-014-3902-7.

8. Konstantinova M, Germanas D, Gudelis A, Plukis A. 2021; Efficiency calibration of high-purity germanium detector using Monte Carlo simulations including coincidence-summing corrections: volume source case. Lith J Phys. 61:66–73. DOI: 10.3952/physics.v61i1.4408.

9. Subercaze A, Sauzedde T, Domergue C, Destouches C, Philibert H, Fausser C, et al. 2022; Effect of the geometrical parameters of an HPGe detector on efficiency calculations using Monte Carlo methods. Nucl Inst Methods Phys Res. 1039:167096. DOI: 10.1016/j.nima.2022.167096.

10. Aviv O, Elia P. 2020; Monte-Carlo simulations of the full-energy-peak efficiency for a broad-energy germanium detector-a comparison between GEANT4 and FLUKA. J Inst. 15:P05016. DOI: 10.1088/1748-0221/15/05/P05016.

11. Andreotti E, Hult M, Marissens G, Lutter G, Garfagnini A, Hemmer S, et al. 2014; Determination of dead-layer variation in HPGe detectors. Appl Radiat Isot. 87:331–335. DOI: 10.1016/j.apradiso.2013.11.046. PMID: 24331853.

12. Bölükdemir MH, Uyar E, Aksoy G, Ünlü H, Dikmen H, Özgür M. 2021; Investigation of shape effects and dead layer thicknesses of a coaxial HPGe crystal on detector efficiency by using PHITS Monte Carlo simulation. Radiat Phys Chem. 189:109746. DOI: 10.1016/j.radphyschem.2021.109746.

13. Liye L, Jizeng M, Franck D, Carlan LD, Binquan Z. 2006; Monte Carlo efficiency transfer method for full energy peak efficiency calibration of three type HPGe detectors: a coaxial N-type, a coaxial P-type and four BEGe detectors. Nucl Inst Methods Phys Res. 564:608–613. DOI: 10.1016/j.nima.2006.03.013.

14. Boson J, Ågren G, Johansson L. 2008; A detailed investigation of HPGe detector response for improved Monte Carlo efficiency calculations. Nucl Inst Methods Phys Res. 587:304–314. DOI: 10.1016/j.nima.2008.01.062.

15. Loan TTH, Ba VN, Thy THN, Hong HTY, Huy NQ. 2018; Determination of the dead-layer thickness for both p- and n-type HPGe detectors using the two-line method. J Radioanal Nucl Chem. 315:95–101. DOI: 10.1007/s10967-017-5637-8.

16. Huy NQ. 2011; Dead-layer thickness effect for gamma spectra measured in an HPGe p-type detector. Nucl Inst Methods Phys Res. 641:101–104. DOI: 10.1016/j.nima.2011.02.097.

17. Elanique A, Marzocchi O, Leone D, Hegenbart L, Breustedt B, Oufni L. 2012; Dead layer thickness characterization of an HPGe detector by measurements and Monte Carlo simulations. Appl Radiat Isotopes. 70:538–542. DOI: 10.1016/j.apradiso.2011.11.014. PMID: 22115878.

18. Kwon NH, Jang YJ, Kim J, Kim KB, Yoo J, Ahn SH, et al. 2021; Measurements of neutron activation and dose rate induced by high-energy medical linear accelerator. Prog Med Phys. 32:145–152. DOI: 10.14316/pmp.2021.32.4.145.