J Rhinol.
2020 Nov;27(2):83-89. 10.18787/jr.2020.00320.
Theory and Practice of Meta-Analysis
- Affiliations
-
- 1Department of Otorhinolaryngology-Head and Neck Surgery, College of Medicine, Konkuk University, Seoul, Korea
- KMID: 2508951
- DOI: http://doi.org/10.18787/jr.2020.00320
Abstract
- Decisions about the utility of an intervention or the validity of a hypothesis should not be based on results of a single study, because different studies provide different results. Hence, a data synthesizing mechanism is required. Meta-analysis is the statistical procedure for combining data from multiple studies. When the treatment effect is consistent across different studies, metaanalysis can identify the common effect. When the treatment effect varies in studies, meta-analysis may identify reasons for variations. Meta-analysis is a powerful tool, though awareness of its limitations and possible errors for correct application are essential.
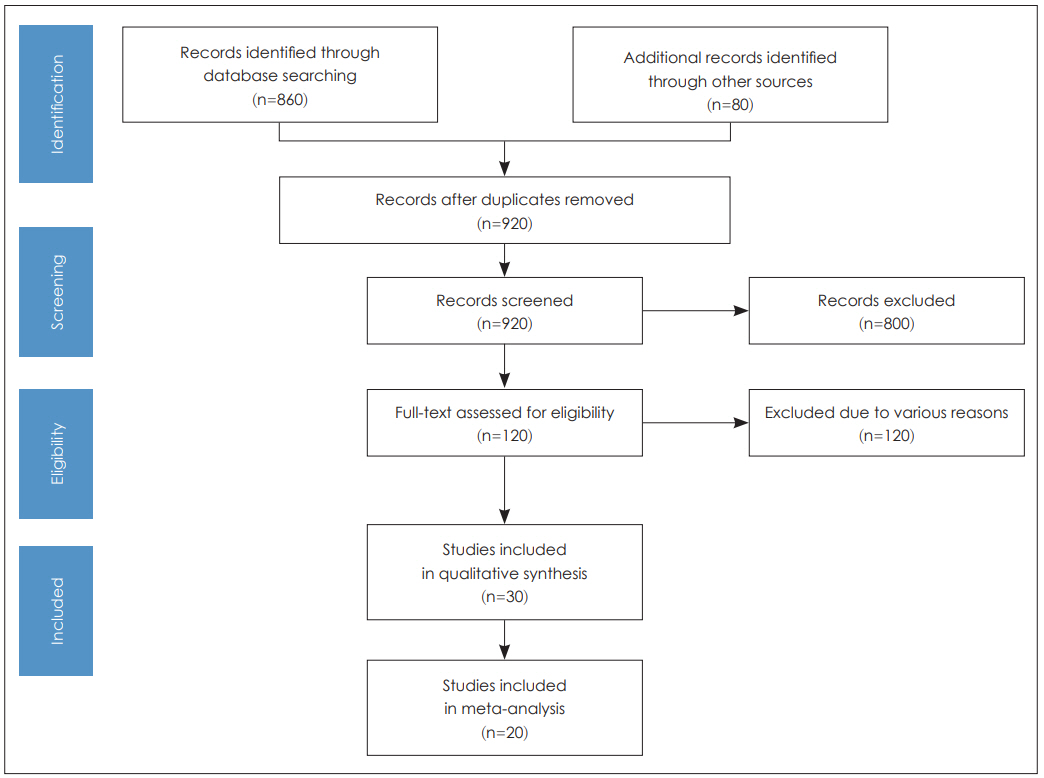
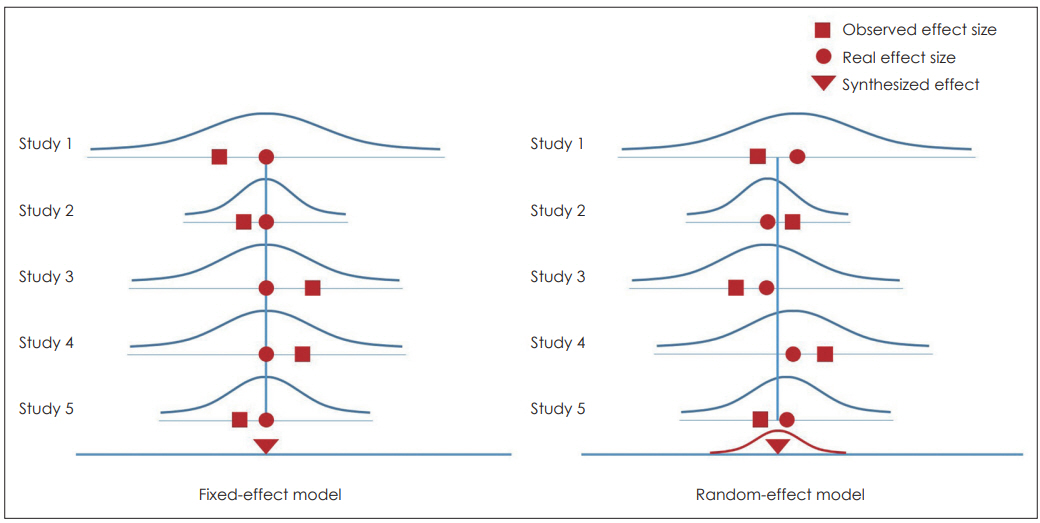
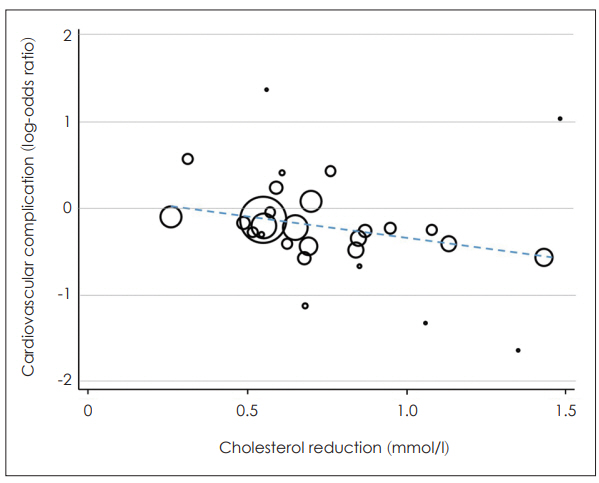
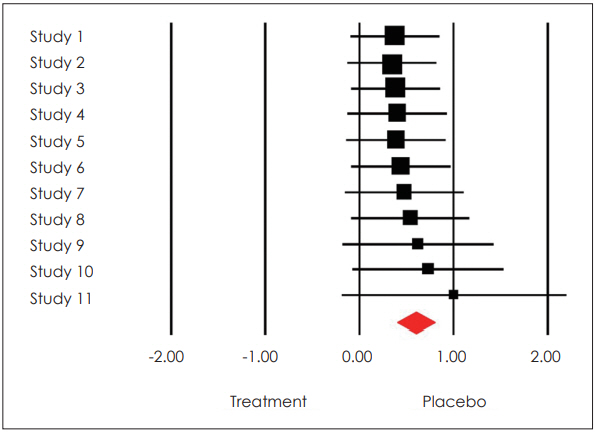
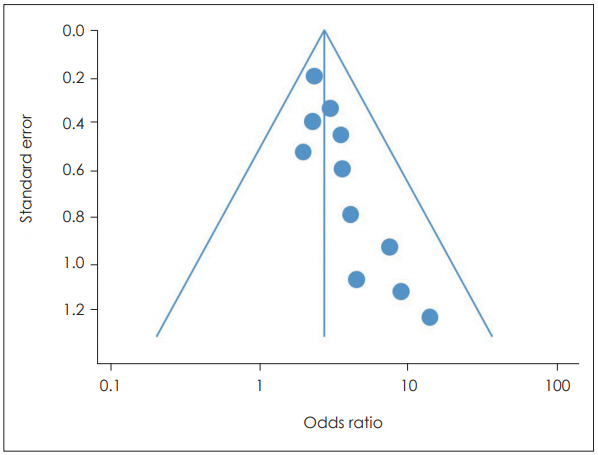
Figure
Cited by 1 articles
-
A Review of a Recent Meta-Analysis Study on Obstructive Sleep Apnea
Bo Yoon Choi, Jin Kook Kim, Jae Hoon Cho
J Rhinol. 2022;29(3):134-140. doi: 10.18787/jr.2022.00422.
Reference
-
1. 황성동. 알기 쉬운 메타분석의 이해. 학지사;2014. all pages.2. Borenstein M, Hedges LV, Higgins JPT, Rpthstein HR. Introduction to meta-analysis. Wiley;2009.3. The Centre for Evidence-Based Medicine develops, promotes and disseminates better evidence for healthcare (https://www.cebm.net/category/ebm-resources/).4. PubMed 검 색 매 뉴 얼(https://ymlib.yonsei.ac.kr/wp-content/uploads/2018/01/PubMed201706-1.pdf).5. 신우종. 체계적 고찰과 메타분석의 개요. Hanyang Med Rev 2015;35:9-17. .