Korean J Orthod.  2020 Sep;50(5):356-359. 10.4041/kjod.2020.50.5.356.

The six geometries revisited

• Kang A
• Musilli M
• Farella M

• KMID: 2506470
• DOI: http://doi.org/10.4041/kjod.2020.50.5.356

Abstract

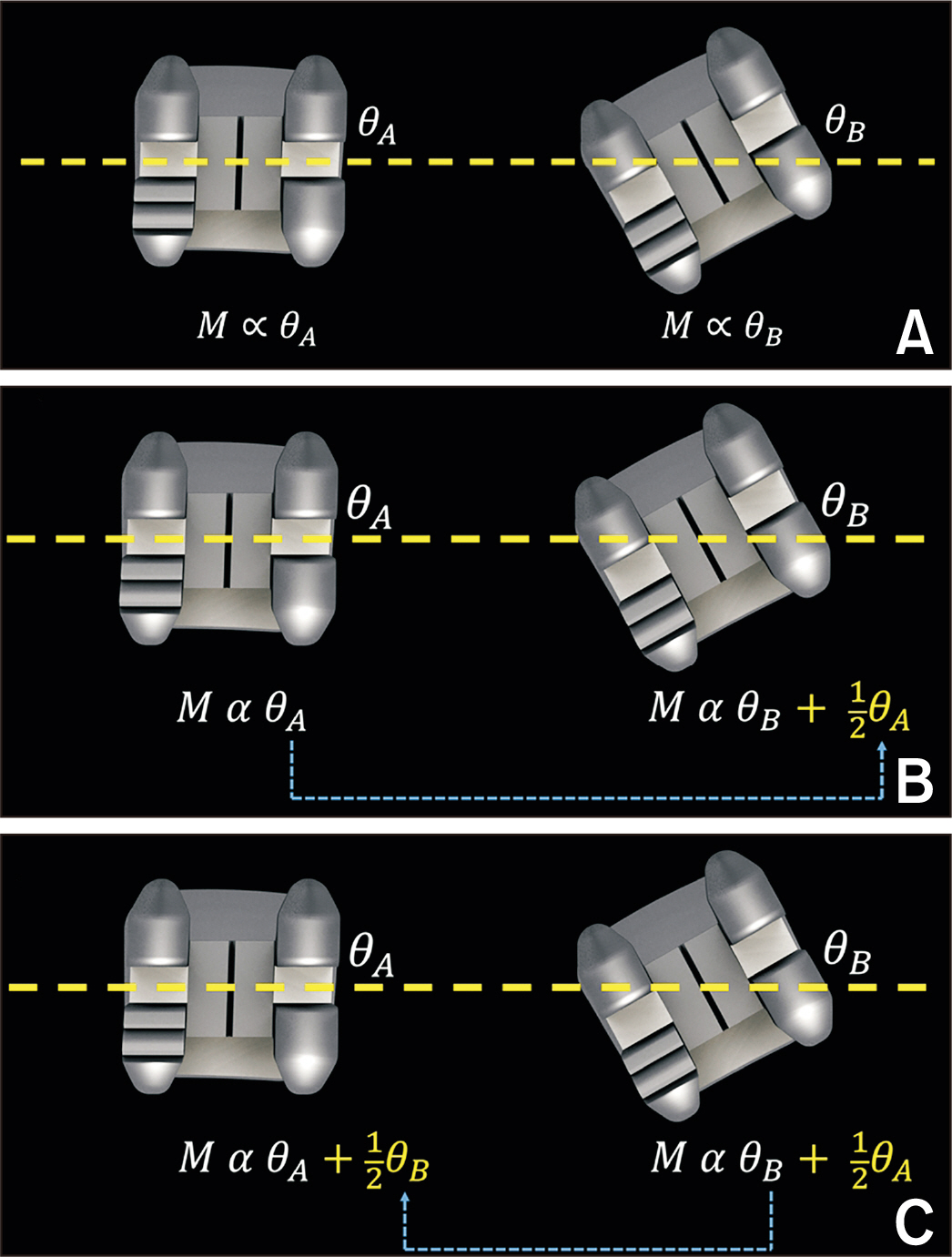
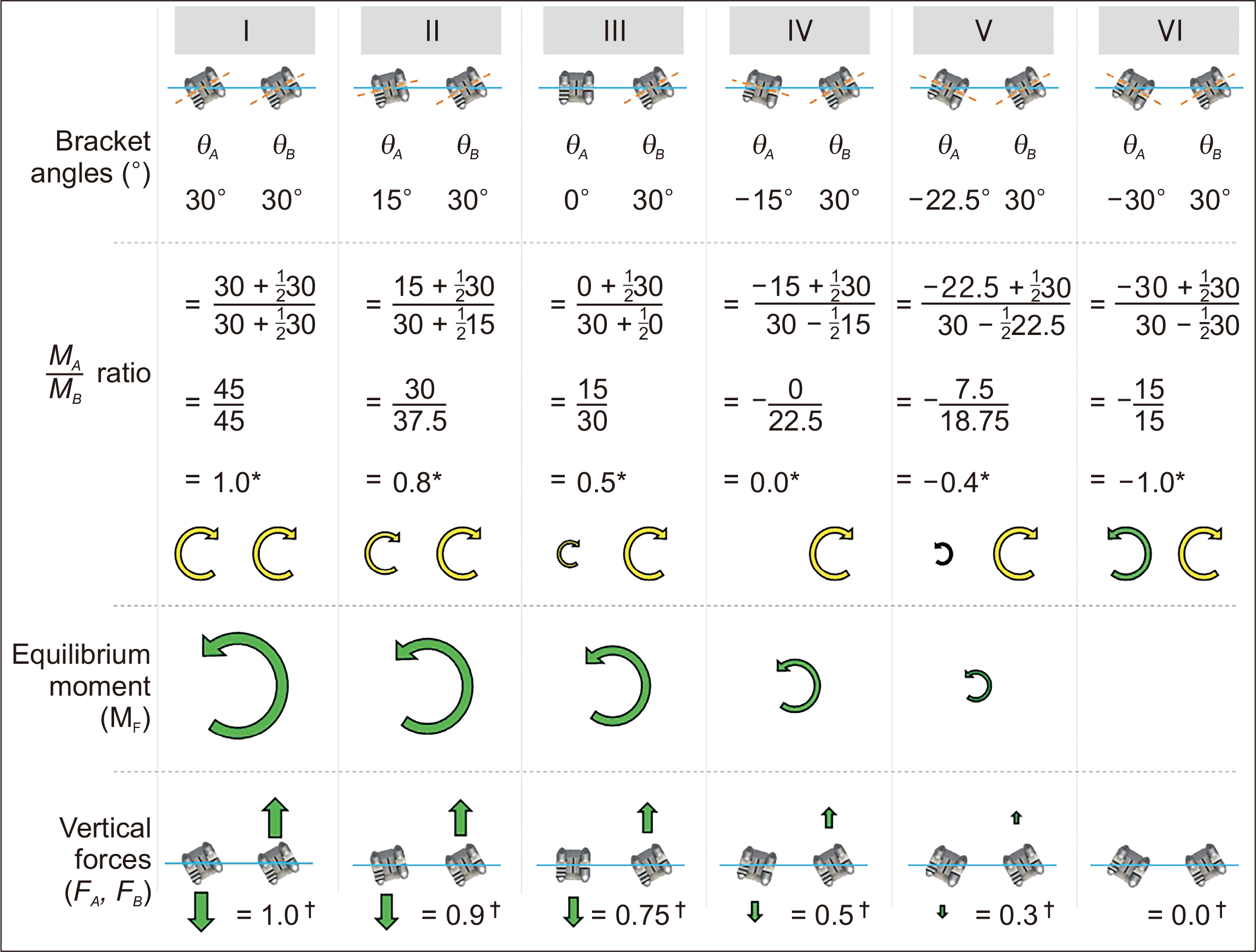
Forces and moments delivered by a straight wire connecting two orthodontic brackets are statically indeterminate and cannot be estimated using the classical equations of static equilibrium. To identify the mechanics of such two-bracket systems, Burstone and Koenig used the principles of linear beam theory to estimate the resulting force systems. In the original publication, however, it remains unclear how the force systems were calculated because no reference or computational details on the underlying principles have been provided. Using the moment carry-over principle and the relative angulation of the brackets, a formula was derived to calculate the relative moments of the two brackets. Because of the moment equilibrium, the vertical forces that exist as a forcecouple on the two brackets can also be calculated. The accuracy of the proposed approach can be validated using previously published empirical data.

Keyword

Tooth movement; Orthodontics; Biomechanics; Bracket geometries

Figure

• 

  Figure 1 A, Moments delivered in a two-bracket system are proportional to the angulation of each bracket. B, The carry-over effect of bracket A affecting bracket B in the same direction and with half the magnitude. C, The carryover effect of bracket B affecting bracket A. M, Moment; θA, angulation of bracket A; θB, angulation of bracket B.

• 

  Figure 2 Computational approach to estimate the moment ratios MAMB for different two-bracket geometries as described by Burstone and Koenig.2 A, Left bracket; B, right bracket; θA, angulation of bracket A; θB, angulation of bracket B. *Note that the estimated ratios for the six geometries are identical to those reported in the original article. †Force magnitudes are relative to the those produced in Geometry I when all other conditions are kept constant.

• 

  Figure 3 A, Moments delivered to each bracket. B, Equilibrium moment existing in the counter-clockwise direction to achieve moment equilibrium. C, Equilibrium moment existing as force couple to produce vertical forces on the brackets. MF, Equilibrium moment; FA, vertical force acting on bracket A; FB, vertical force on bracket B.

Reference

1. Lindauer J. 2001; The basics of orthodontic mechanics. Semin Orthod. 7:2–15. DOI: 10.1053/sodo.2001.21053.

2. Burstone CJ, Koenig HA. 1974; Force systems from an ideal arch. Am J Orthod. 65:270–89. DOI: 10.1016/S0002-9416(74)90332-7. PMID: 2923317.

3. Burstone CJ, Choy K. Burstone CJ, Choy K, editors. 2015. Forces from wires and brackets. The biomechanical foundation of clinical orthodontics. Quintessence Publishing;Chicago: p. 332.

4. Cross H. 1930. Analysis of continuous frames by distributing fixed-end moments. Paper presented at: American Society of Civil Engineers Annual Convention. 1930 Jul 9-11; American Society of Civil Engineers;Cleveland, USA. New York: p. 919–28.