Korean J Orthod.  2016 Nov;46(6):356-363. 10.4041/kjod.2016.46.6.356.

Reference points suitable for evaluation of the additional arch length required for leveling the curve of Spee

• Cho YH
• Lim SH
• Gang SN

• KMID: 2426679
• DOI: http://doi.org/10.4041/kjod.2016.46.6.356

Abstract

OBJECTIVE
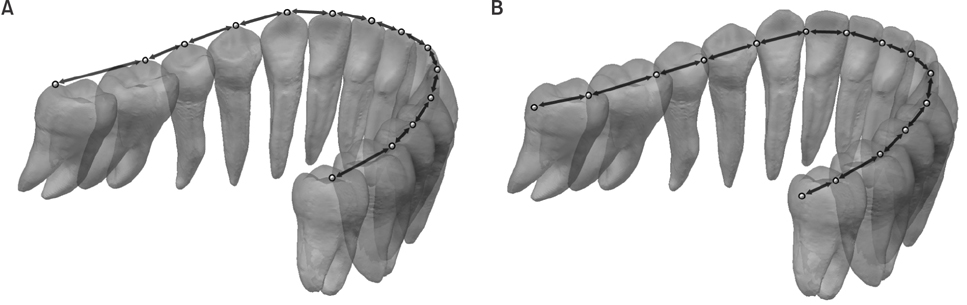
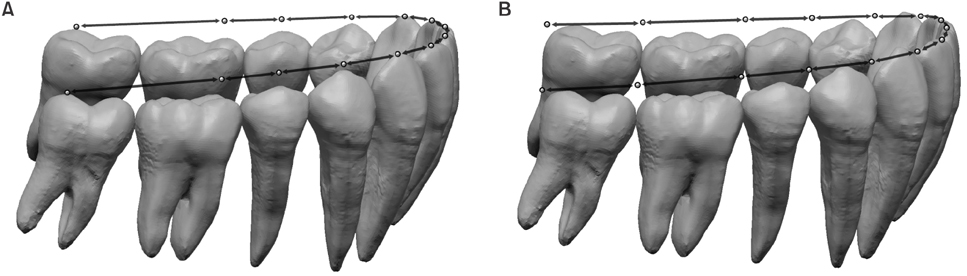
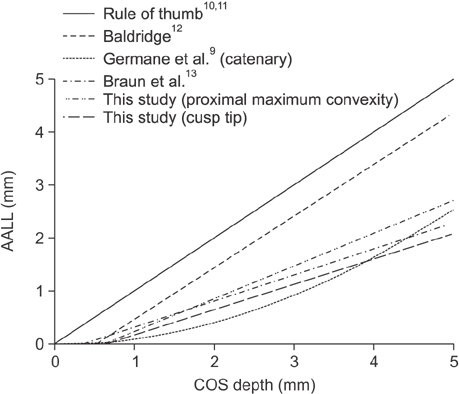
The additional arch length required for leveling (AALL) the curve of Spee (COS) can be estimated by subtracting the two-dimensional (2D) arch circumference, which is the projection of the three-dimensional (3D) arch circumference onto the occlusal plane, from the 3D arch circumference, which represents the arch length after leveling the COS. The purpose of this study was to determine whether the cusp tips or proximal maximum convexities are more appropriate reference points for estimating the AALL.
METHODS
Sixteen model setups of the mandibular arch with COS depths ranging from 0 mm to 4.7 mm were constructed using digital simulation. Arch circumferences in 2D and 3D were measured from the cusp tips and proximal maximum convexities and used to calculate the AALL. The values obtained using the two reference points were compared with the paired t-test.
RESULTS
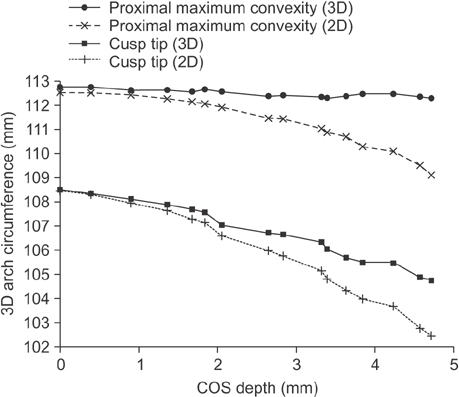
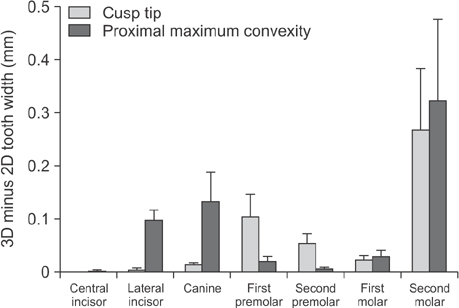
Although the 3D arch circumference should be constant regardless of the COS depth, it decreased by 3.8 mm in cusp tip measurements and by 0.4 mm in proximal maximum convexity measurements as the COS deepened to 4.7 mm. AALL values calculated using the cusp tips as reference points were significantly smaller than those calculated using the proximal maximum convexities (p = 0.002).
CONCLUSIONS
The AALL is underestimated when the cusp tips are used as measurement reference points; the AALL can be measured more accurately using the proximal maximum convexities.

Keyword

Digital models; Dental cast analysis; 3-Dimensional diagnosis and treatment planning; Curve of Spee

MeSH Terms

Dental Occlusion

Figure

• 

  Figure 1 The three-dimensional (3D) arch circumference is calculated as the sum of the 3D tooth widths, corresponding to the distances between adjacent reference points, which are shown as dots in A and B. A, 3D tooth widths measured using the cusp tip as a reference; B, 3D tooth widths measured using the proximal maximum convexity as a reference.

• 

  Figure 2 The two-dimensional (2D) arch circumference is calculated as the sum of the 2D tooth widths, which are projections of the three-dimensional tooth widths onto the occlusal plane. A, 2D tooth widths measured using the cusp tip as a reference; B, 2D tooth widths measured using the proximal maximum convexity as a reference.

• 

  Figure 3 Changes in three-dimensional (3D) and two-dimensional (2D) arch circumferences according to the use of cusp tips and proximal maximum convexities as references. The 3D arch circumference decreased by 3.8 mm in the cusp tip measurements and by 0.4 mm in the proximal convexity measurements as the curve of Spee (COS) increased from 0 mm to 4.7 mm. The difference between the 3D arch circumference and 2D arch circumference is the AALL. Data are mean and standard deviation values. AALL, The amount of additional arch length required for leveling the COS.

• 

  Figure 4 Measurements of the three-dimensional (3D) tooth width minus the two-dimensional (2D) tooth width for each tooth. In the cusp tip measurements, the widths were measured between the cusp tips of adjacent teeth, while in the proximal maximum convexity measurements, they were measured between the mesial and distal maximum convexities. Mean values from 16 setup models are shown.

• 

  Figure 5 A comparison of estimations of the AALL from various studies is shown. AALL, The amount of additional arch length required for leveling the COS; COS, curve of Spee.

Reference

1. Spee FG, Biedenbach MA, Hotz M, Hitchcock HP. The gliding path of the mandible along the skull. J Am Dent Assoc. 1980; 100:670–675.

2. Hitchcock HP. The curve of Spee in stone age man. Am J Orthod. 1983; 84:248–253.

3. Marshall SD, Caspersen M, Hardinger RR, Franciscus RG, Aquilino SA, Southard TE. Development of the curve of Spee. Am J Orthod Dentofacial Orthop. 2008; 134:344–352.

4. Carter GA, McNamara JA Jr. Longitudinal dental arch changes in adults. Am J Orthod Dentofacial Orthop. 1998; 114:88–99.

5. Bishara SE, Jakobsen JR, Treder JE, Stasi MJ. Changes in the maxillary and mandibular tooth size-arch length relationship from early adolescence to early adulthood. A longitudinal study. Am J Orthod Dentofacial Orthop. 1989; 95:46–59.

6. Burstone CJ, Marcotte MR. Problem solving in orthodontics: Goal-oriented treatment strategies. Chicago: Quintessence Pub;2000. p. 181–183.

7. Andrews LF. The six keys to normal occlusion. Am J Orthod. 1972; 62:296–309.

8. AlQabandi AK, Sadowsky C, BeGole EA. A comparison of the effects of rectangular and round arch wires in leveling the curve of Spee. Am J Orthod Dentofacial Orthop. 1999; 116:522–529.

9. Germane N, Staggers JA, Rubenstein L, Revere JT. Arch length considerations due to the curve of Spee: a mathematical model. Am J Orthod Dentofacial Orthop. 1992; 102:251–255.

10. Proffit WR, Epker BN. Treatment planning for dentofacial deformities. In : Bell WH, Proffit WR, White RP, editors. Surgical correction of dentofacial deformities. Philadelphia: WB Saunders;1980. p. 167.

11. Proffit WR, Ackerman J. Diagnosis and treatment planning in orthodontics. In : Graber TM, editor. Orthodontics: current principals and techniques. St. Louis: CV Mosby;1986. p. 62–67.

12. Baldridge DW. Leveling the curve of Spee: its effect on mandibular arch length. JPO J Pract Orthod. 1969; 3:26–41.

13. Braun S, Hnat WP, Johnson BE. The curve of Spee revisited. Am J Orthod Dentofacial Orthop. 1996; 110:206–210.

14. Shahid F, Alam MK, Khamis MF. New prediction equations for the estimation of maxillary mandibular canine and premolar widths from mandibular incisors and mandibular first permanent molar widths: A digital model study. Korean J Orthod. 2016; 46:171–179.

15. Kim J, Lagravére MO. Accuracy of Bolton analysis measured in laser scanned digital models compared with plaster models (gold standard) and cone-beam computer tomography images. Korean J Orthod. 2016; 46:13–19.

16. Garcia R. Leveling the curve of Spee: a new prediction formula. J Charles H. Tweed Int Found. 1985; 13:65–72.

17. Veli I, Ozturk MA, Uysal T. Curve of Spee and its relationship to vertical eruption of teeth among different malocclusion groups. Am J Orthod Dentofacial Orthop. 2015; 147:305–312.

18. Shannon KR, Nanda RS. Changes in the curve of Spee with treatment and at 2 years posttreatment. Am J Orthod Dentofacial Orthop. 2004; 125:589–596.

19. Cheon SH, Park YH, Paik KS, Ahn SJ, Hayashi K, Yi WJ, et al. Relationship between the curve of Spee and dentofacial morphology evaluated with a 3-dimensional reconstruction method in Korean adults. Am J Orthod Dentofacial Orthop. 2008; 133:640.e7–640.e14.

20. Dahlberg G. Statistical methods for medical and biological students. London: George Allen & Unwin Ltd.;1940. p. 122–132.

21. Frost HM. The biology of fracture healing. An overview for clinicians. Part I. Clin Orthop Relat Res. 1989; (248):283–293.

22. Yaffe A, Fine N, Binderman I. Regional accelerated phenomenon in the mandible following mucoperiosteal flap surgery. J Periodontol. 1994; 65:79–83.

23. Woods M. A reassessment of space requirements for lower arch leveling. J Clin Orthod. 1986; 20:770–778.