Prog Med Phys.  2016 Mar;27(1):1-7. 10.14316/pmp.2016.27.1.1.

Compressed-sensing (CS)-based Image Deblurring Scheme with a Total Variation Regularization Penalty for Improving Image Characteristics in Digital Tomosynthesis (DTS)

• Je U
• Kim K
• Cho H
• Kim G
• Park S
• Lim H
• Park C
• Park Y

• KMID: 2161932
• DOI: http://doi.org/10.14316/pmp.2016.27.1.1

Abstract

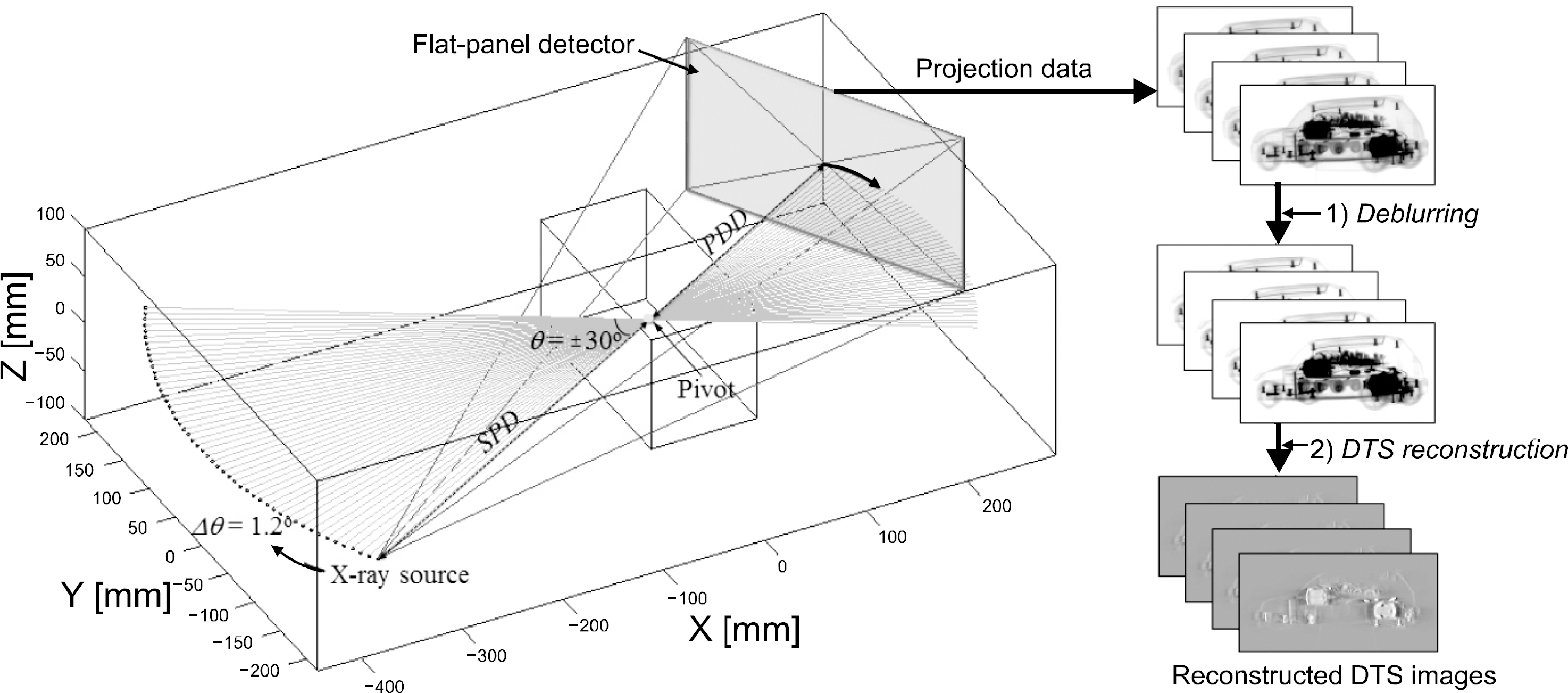
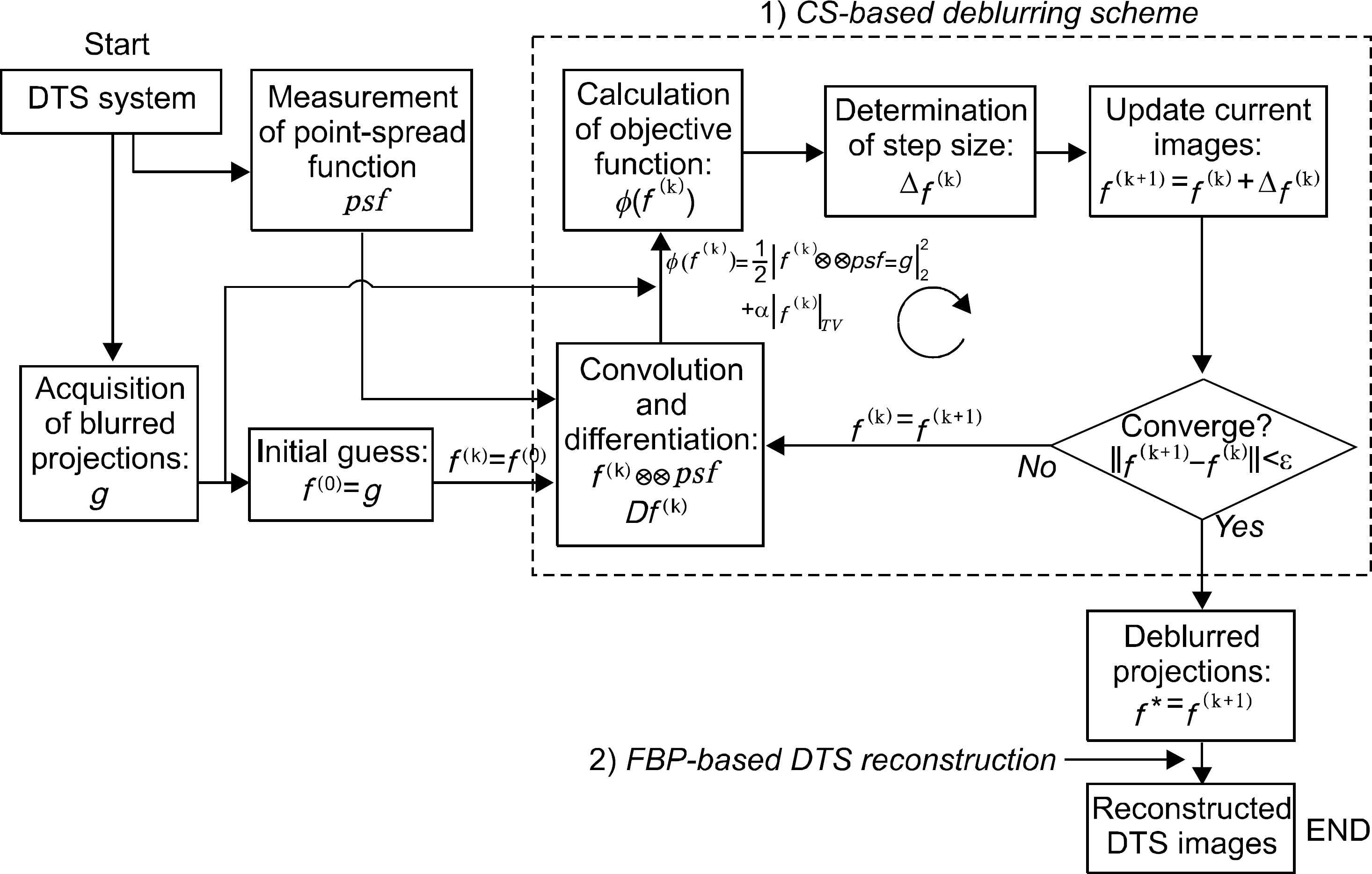
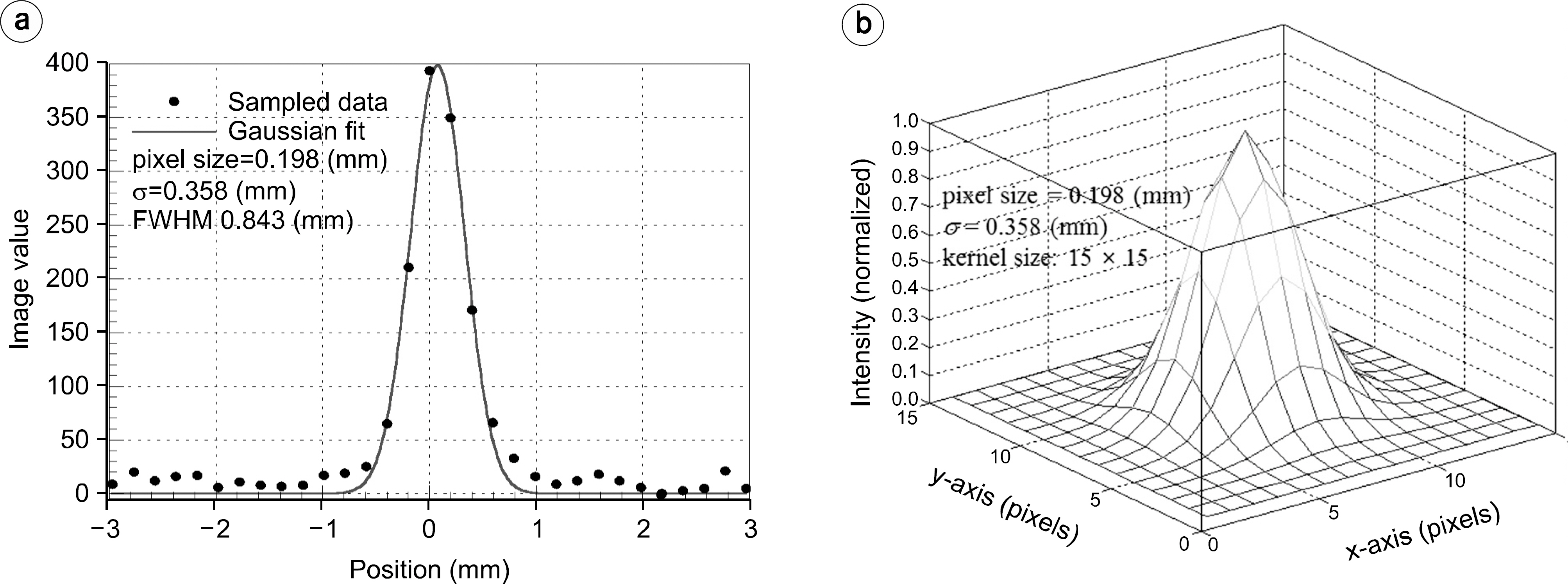
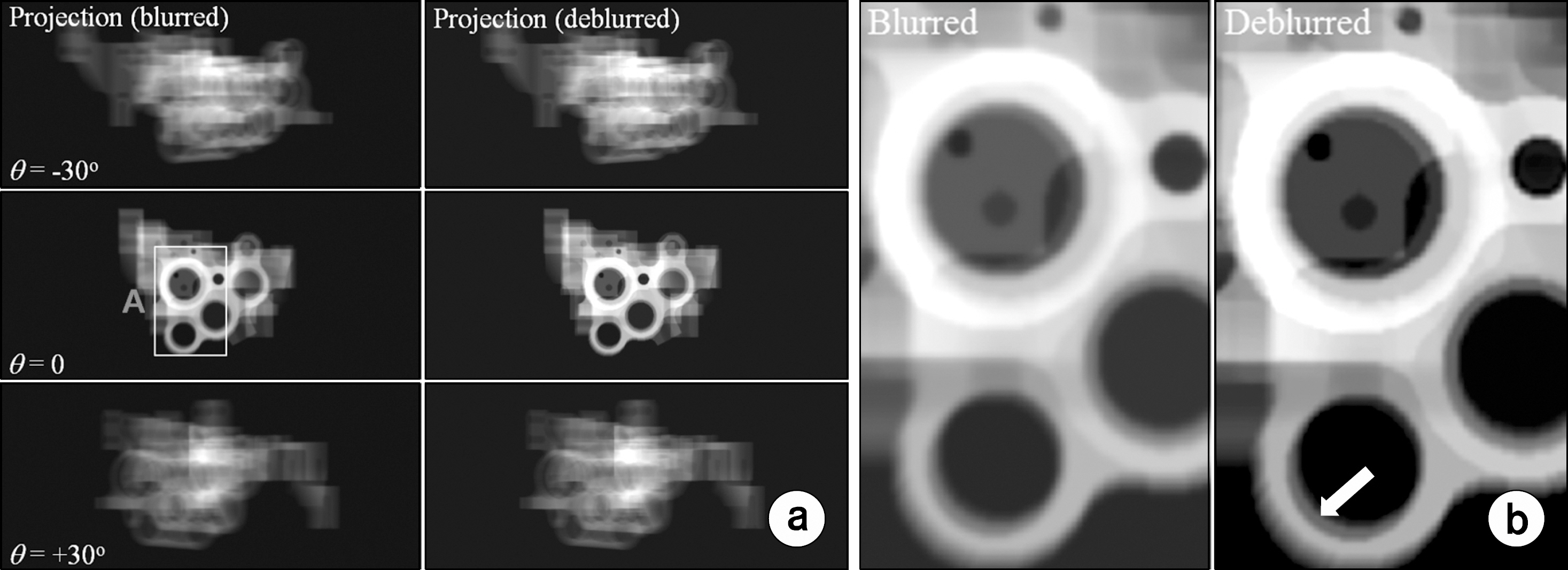
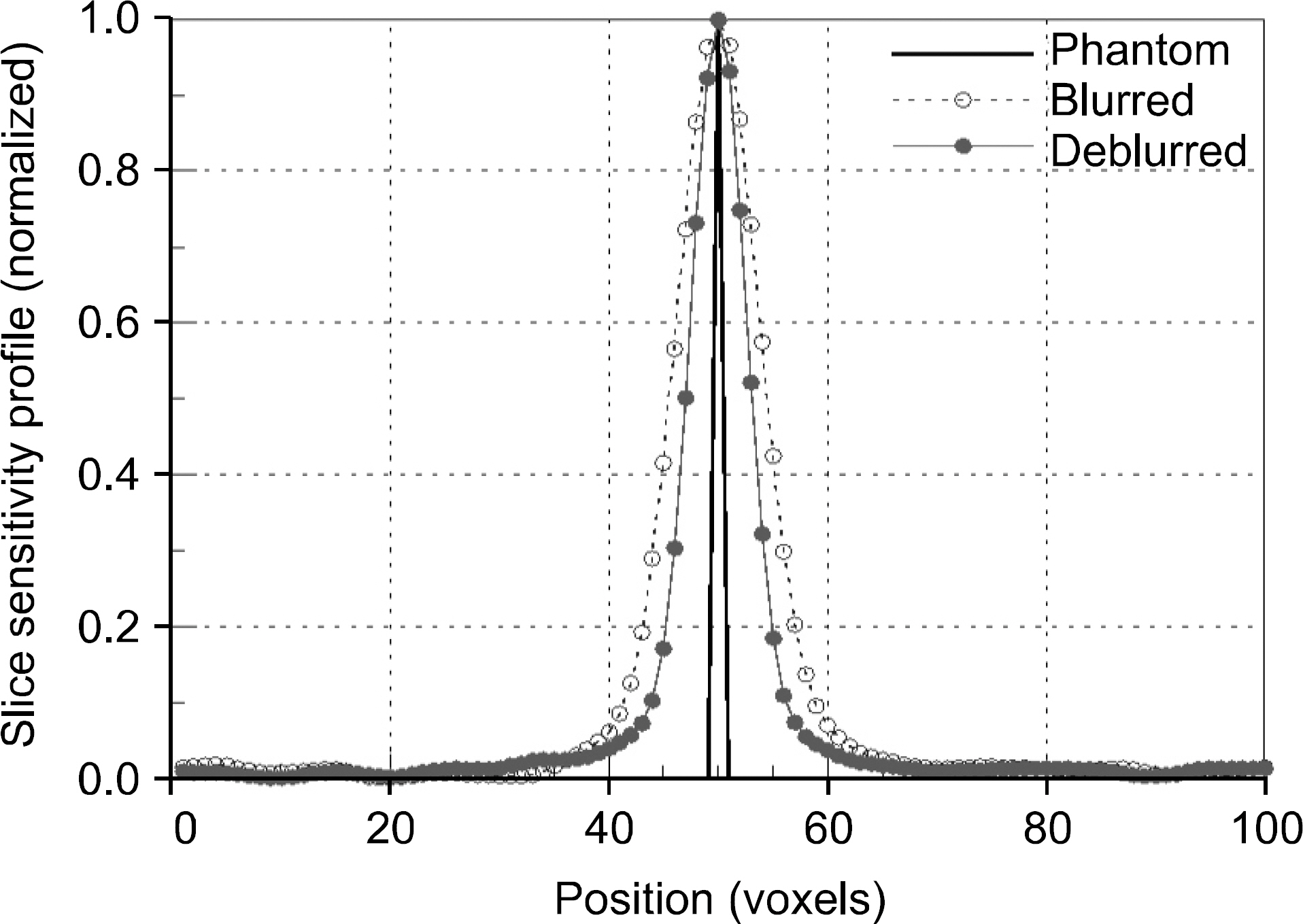
In this work, we considered a compressed-sensing (CS)-based image deblurring scheme with a total-variation (TV) regularization penalty for improving image characteristics in digital tomosynthesis (DTS). We implemented the proposed image deblurring algorithm and performed a systematic simulation to demonstrate its viability. We also performed an experiment by using a table-top setup which consists of an x-ray tube operated at 90 kVp, 6 mAs and a CMOS-type flat-panel detector having a 198-µm pixel resolution. In the both simulation and experiment, 51 projection images were taken with a tomographic angle range of θ=60° and an angle step of Δθ=1.2° and then deblurred by using the proposed deblurring algorithm before performing the common filtered-backprojection (FBP)-based DTS reconstruction. According to our results, the image sharpness of the recovered x-ray images and the reconstructed DTS images were significantly improved and the cross-plane spatial resolution in DTS was also improved by a factor of about 1.4. Thus the proposed deblurring scheme appears to be effective for the blurring problems in both conventional radiography and DTS and is applicable to improve the present image characteristics.

Keyword

Compressed-sensing (CS); Digital tomosynthesis (DTS); Deblurring; Total variation (TV)

MeSH Terms

Radiography

Figure

• 

  Fig. 1. Schematic illustration of a typical DTS geometry in which an x-ray source and a flat-panel detector move together in an arc around the pivot during the projection data acquisition.

• 

  Fig. 2. Simplified flowchart of the CS-based deblurring scheme in DTS. The acquired projection images are deblurred through the CS-based scheme before performing the common FBP-based DTS reconstruction.

• 

  Fig. 3. (a) 3D numerical phantom of a pump casting used in the simulation and (b) the table-top setup that we established for the experiment.

• 

  Fig. 4. (a) Measured 1D LSF curve with a Gaussian fit, and (b) the resultant 2D blur kernel having a filter size of 15×15. The same blur kernel was used in the both simulation and the experiment.

• 

  Fig. 5. (a) Some examples of the blurred (left) and the deblurred (right) projection images of the pump casting and (b) their enlarged images indicated by the box A in (a). Only three projection images (i.e., for θ= −30 o, 0, and ＋30 o) out of the 51 are indicated for simplicity).

• 

  Fig. 6. Some examples of the reconstructed DTS images of the pump casting from the front side (top) to the rear side (bottom) for no blurring, blurring, and deblurring cases. Only 4 slices out of the 426 are indicated for simpli-city. The phantom slice images (the leftmost) are also indicated as the reference.

• 

  Fig. 7. The enlarged DTS images indicated by the box A in Fig. 6 for no blurring, blurring, and deblurring cases. The phantom slice image (upper left) is also indicated as the reference.

• 

  Fig. 8. An example of the reconstructed DTS images of the toy car (i.e., for x=306 th slice) for (a) blurring and (b) deblurring cases.

• 

  Fig. 9. The measured SSP curves along the x– axis from the reconstructed DTS images of the small thin-square phantom. Here the intensity profile of the phantom in x is also indicated as the reference.

Reference

References

1. Dobbins J., Godfrey D.Digitalx-raytomosynthesis: current state of the art and clinical potential. Phys.Med.Biol. 48(19):R65–106. 2003.

2. Xu F., Helfen L., Baumbach T., Suhonen H.Comparison of image quality incomputed laminography and tomography. Opt. Express. 20(2):794–806. 2012.

3. Choi K., Wang J., Zhu L., Suh T. S., Boyd S., Xing L.Compressed sensing based cone-beam computed tomography reconstruction with a first-order method. Med. Phys. 37:5113–5125. 2010.

4. Xu H., Huang T., Lv X., Liu J.The Implementation of LSMR in Image Deblurring. Appl.Math.Inf. 8(6):3041–3048. 2014.

5. Figueiredo M., Nowak R.An EM algorithm for wave-let-based image restoration. IEEE Trans. Image Process. 12:906–916. 2003.

6. Li X.Fine-granularity and spatially-adaptive regularization for projection-based image deblurring. IEEE Trans. Image Process. 20:971–983. 2011.

7. Babacan S., Molina R., Katsaggelos A.Parameter estimation in TV image rest orationusingvariationaldistribution approximation. IEEE Trans. Image Process. 17(3):326–339. 2008.

8. Park J., Song B. Y., Kim J. S., et al. Fast compressed sensing-based CBCT reconstruction using Barzilai-Borweinfor-mulationfor application toonline IGRT. Med.Phys. 39(3):1207–1217. 2012.

9. Oh J. E., Cho H. S., Kim D. S., Choi S. I., Je U. K.Application of digital to mosynthesis(DTS) of optimal deblurring filters for dentalx-ray imaging. Jof the Korean Phys.Soc. 60(6):1161–1166. 2012.