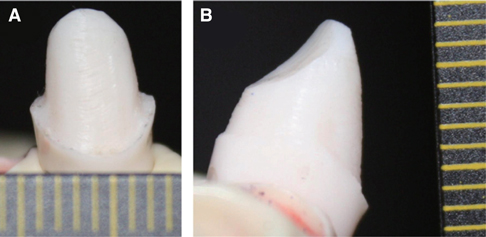
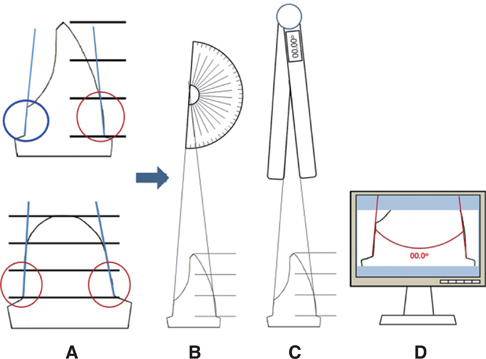
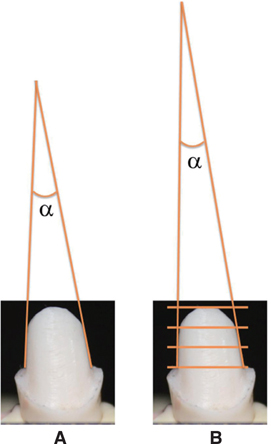
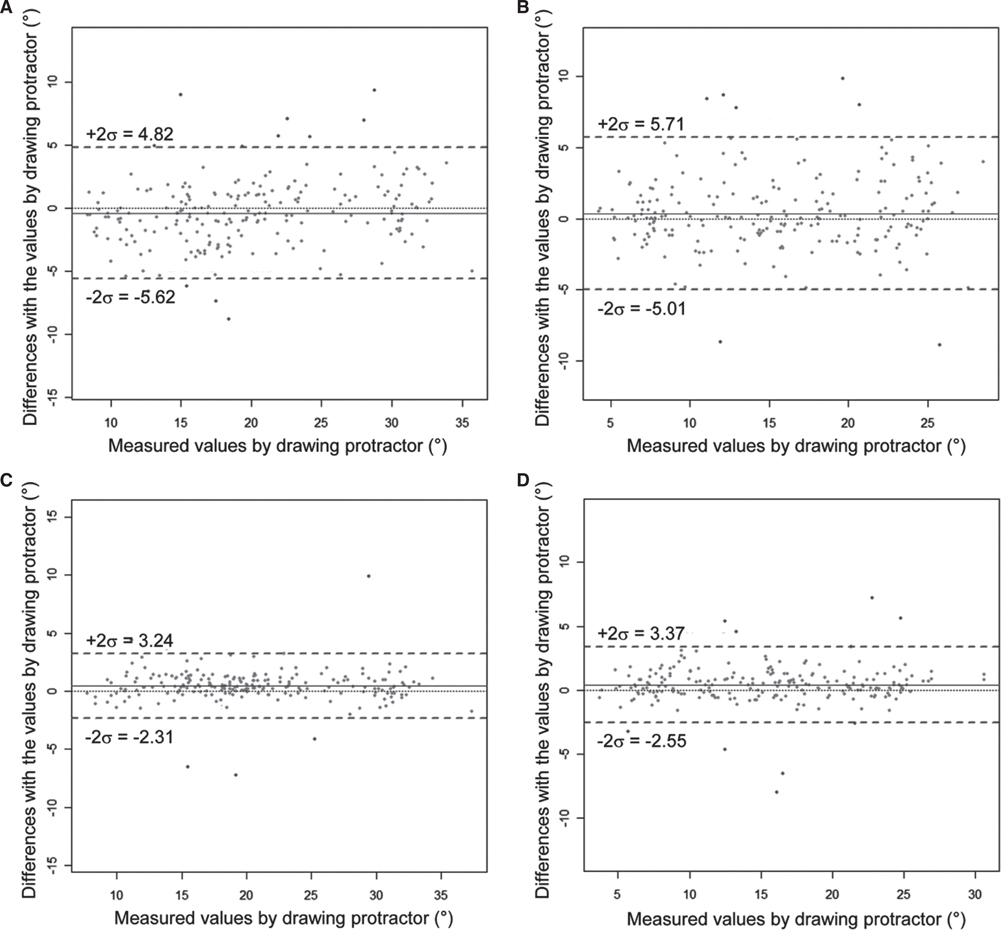
J Adv Prosthodont.  2014 Jun;6(3):185-193. 10.4047/jap.2014.6.3.185.

The reliability of an easy measuring method for abutment convergence angle with a computer-aided design (CAD) system

• Seo YJ
• Kwon TK
• Han JS
• Lee JB
• Kim SH
• Yeo IS

• KMID: 2118229
• DOI: http://doi.org/10.4047/jap.2014.6.3.185

Abstract

PURPOSE
The purpose of this study was to evaluate the intra-rater reliability and inter-rater reliability of three different methods using a drawing protractor, a digital protractor after tracing, and a CAD system.
MATERIALS AND METHODS
Twenty-four artificial abutments that had been prepared by dental students were used in this study. Three dental students measured the convergence angles by each method three times. Bland-Altman plots were applied to examine the overall reliability by comparing the traditional tracing method with a new method using the CAD system. Intraclass Correlation Coefficients (ICC) evaluated intra-rater reliability and inter-rater reliability.
RESULTS
All three methods exhibited high intra-rater and inter-rater reliability (ICC>0.80, P<.05). Measurements with the CAD system showed the highest intra-rater reliability. In addition, it showed improved inter-rater reliability compared with the traditional tracing methods.
CONCLUSION
Based on the results of this study, the CAD system may be an easy and reliable tool for measuring the abutment convergence angle.

Keyword

Computer-aided design; Convergence angle; Prosthodontic tooth preparation; Validation studies; Dental abutments

MeSH Terms

Computer-Aided Design*
Dental Abutments
Humans
Students, Dental
Tooth Preparation, Prosthodontic

Figure

• 

  Fig. 1 The images provided to the raters. (A) A printed image for measuring the mesio-distal convergence angle, and (B) A printed image for measuring the bucco-lingual convergence angle by tracing or CAD.

• 

  Fig. 2 Schematic diagram of the measuring methods. (A) The occlusal convergence angle was measured based on the inclination of the cervical third (red circles). In case of the lingual surface, the end of the cingulum was determined as a reference point (blue circle). Three different methods were used to measure the occlusal convergence angles. After tracing the images following the magnification of the pictures, the abutment occlusal convergence angles were measured using a drawing protractor (B) and a digital protractor (C). (D) represents measuring by CAD on the monitor.

• 

  Fig. 3 The definition of the abutment occlusal convergence angle in this study. The occlusal convergence angle is usually selected as shown in (A). However, the angle was defined in this study as in (B), based on the inclination of the cervical third. Comparison between (A) and (B) shows that the occlusal convergence angles are different from each other, depending on the selected portion of the prepared wall. α: abutment occlusal convergence angle.

• 

  Fig. 4 The measurement of the abutment occlusal convergence angle by CAD. The two tangent lines (red solid lines) are mesio-distally established to the cervical third of the abutment. The software virtually extends the tangent lines to converge (white dashed lines) and calculates the angle between the tangent lines. Therefore, additional space, which the tracing method requires, is unnecessary.

• 

  Fig. 5 Bland-Altman plots. (A) The distribution of the bucco-lingual convergence angle differences between the measurements by CAD and drawing protractor, (B) The distribution of the mesio-distal convergence angle differences between the measurements by CAD and drawing protractor, (C) The distribution of the bucco-lingual convergence angle differences between the measurements by digital protractor and drawing protractor, and (D) The distribution of the mesio-distal convergence angle differences between the measurements by digital protractor and drawing protractor are shown. The solid lines represent the mean values of the differences between the two methods. The dashed lines are ±2s of the measured value differences between two methods. s; standard deviation.

• 

  Fig. 6 Inter-rater reliabilities of the convergence angles measured at mesio-distal direction (A), and at bucco-lingual direction (B), according to the measuring methods (n = 72). The black rods show 95% of confidence intervals. All ICCs are over 0.80, which means perfect agreement. Especially notice that the ICCs calculated for the CAD group are over 0.90 both at mesio-distal and at bucco-lingual directions.

• 

  Fig. 7 The paired t-test results for the convergence angles measured between mesio-distally and bucco-lingually. Means and standard deviation (SD) of the abutment convergence angles are shown according to the measuring methods. Data are expressed as the mean ± SD (n = 216). *P<.05.

Reference

1. The glossary of prosthodontic terms. J Prosthet Dent. 2005; 94:10–92.

2. Jørgensen KD. The relationship between retention and convergence angle in cemented veneer crowns. Acta Odontol Scand. 1955; 13:35–40.

3. Kaufman EG, Coelho DH, Colin L. Factors influencing the retention of cemented gold castings. J Prosthet Dent. 1961; 11:487–502.

4. Goodacre CJ, Campagni WV, Aquilino SA. Tooth preparations for complete crowns: an art form based on scientific principles. J Prosthet Dent. 2001; 85:363–376.

5. Wilson AH Jr, Chan DC. The relationship between preparation convergence and retention of extracoronal retainers. J Prosthodont. 1994; 3:74–78.

6. Weed RM. Determining adequate crown convergence. Tex Dent J. 1980; 98:14–16.

7. Al-Omari WM, Al-Wahadni AM. Convergence angle, occlusal reduction, and finish line depth of full-crown preparations made by dental students. Quintessence Int. 2004; 35:287–293.

8. el-Ebrashi MK, Craig RG, Peyton FA. Experimental stress analysis of dental restorations. VI. The concept of proximal reduction in compound restorations. J Prosthet Dent. 1969; 22:663–670.

9. Weed RM, Baez RJ. A method for determining adequate resistance form of complete cast crown preparations. J Prosthet Dent. 1984; 52:330–334.

10. Lewis RM, Owen MM. A mathematical solution of a problem in full crown construction. J Am Dent Assoc. 1959; 59:943–947.

11. Shillingburg HT, Hobo S, Whitsett LD, Brackett SE. Fundamentals of fixed prosthodontics. In : Bateman LA, editor. Principles of tooth preparations. 3rd ed. Chicago: Quintessence Pub. Co.;1997. p. 119–138.

12. Chandra Shekar S, Giridhar K, Suhas Rao K. An in vitro study to evaluate the retention of complete crowns prepared with five different tapers and luted with two different cements. J Indian Prosthodont Soc. 2010; 10:89–95.

13. Annerstedt A, Engström U, Hansson A, Jansson T, Karlsson S, Liljhagen H, Lindquist E, Rydhammar E, Tyreman-Bandhede M, Svensson P, Wandel U. Axial wall convergence of full veneer crown preparations. Documented for dental students and general practitioners. Acta Odontol Scand. 1996; 54:109–112.

14. Mack PJ. A theoretical and clinical investigation into the taper achieved on crown and inlay preparations. J Oral Rehabil. 1980; 7:255–265.

15. Ohm E, Silness J. The convergence angle in teeth prepared for artificial crowns. J Oral Rehabil. 1978; 5:371–375.

16. Leempoel PJ, Lemmens PL, Snoek PA, van't Hof MA. The convergence angle of tooth preparations for complete crowns. J Prosthet Dent. 1987; 58:414–416.

17. Smith CT, Gary JJ, Conkin JE, Franks HL. Effective taper criterion for the full veneer crown preparation in preclinical prosthodontics. J Prosthodont. 1999; 8:196–200.

18. Velasquez-Plata D, Andres CJ. The art of crown preparation: a review of principles. J Indiana Dent Assoc. 1996; 75:6–11.

19. Ayad MF, Maghrabi AA, Rosenstiel SF. Assessment of convergence angles of tooth preparations for complete crowns among dental students. J Dent. 2005; 33:633–638.

20. Dodge WW, Weed RM, Baez RJ, Buchanan RN. The effect of convergence angle on retention and resistance form. Quintessence Int. 1985; 16:191–194.

21. Nordlander J, Weir D, Stoffer W, Ochi S. The taper of clinical preparations for fixed prosthodontics. J Prosthet Dent. 1988; 60:148–151.

22. Noonan JE Jr, Goldfogel MH. Convergence of the axial walls of full veneer crown preparations in a dental school environment. J Prosthet Dent. 1991; 66:706–708.

23. Kent WA, Shillingburg HT Jr, Duncanson MG Jr. Taper of clinical preparations for cast restorations. Quintessence Int. 1988; 19:339–345.

24. Okuyama Y, Kasahara S, Kimura K. Quantitative evaluation of axial wall taper in prepared artificial teeth. J Oral Sci. 2005; 47:129–133.

25. Dorriz H, Nokar S, Baghai Naini R, Madadi A. The convergence angle of full-coverage crown preparations made by dental students. J Dent (Tehran). 2008; 5:37–41.

26. de Vet HC, Terwee CB, Knol DL, Bouter LM. When to use agreement versus reliability measures. J Clin Epidemiol. 2006; 59:1033–1039.

27. Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979; 86:420–428.

28. Weir JP. Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J Strength Cond Res. 2005; 19:231–240.

29. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977; 33:159–174.