Korean J Transplant.  2020 Sep;34(3):167-177. 10.4285/kjt.2020.34.3.167.

Mathematical model for early functional recovery pattern of kidney transplant recipients using serum creatinine

• Bang JB
• Oh CK

• KMID: 2507161
• DOI: http://doi.org/10.4285/kjt.2020.34.3.167

Abstract

Background
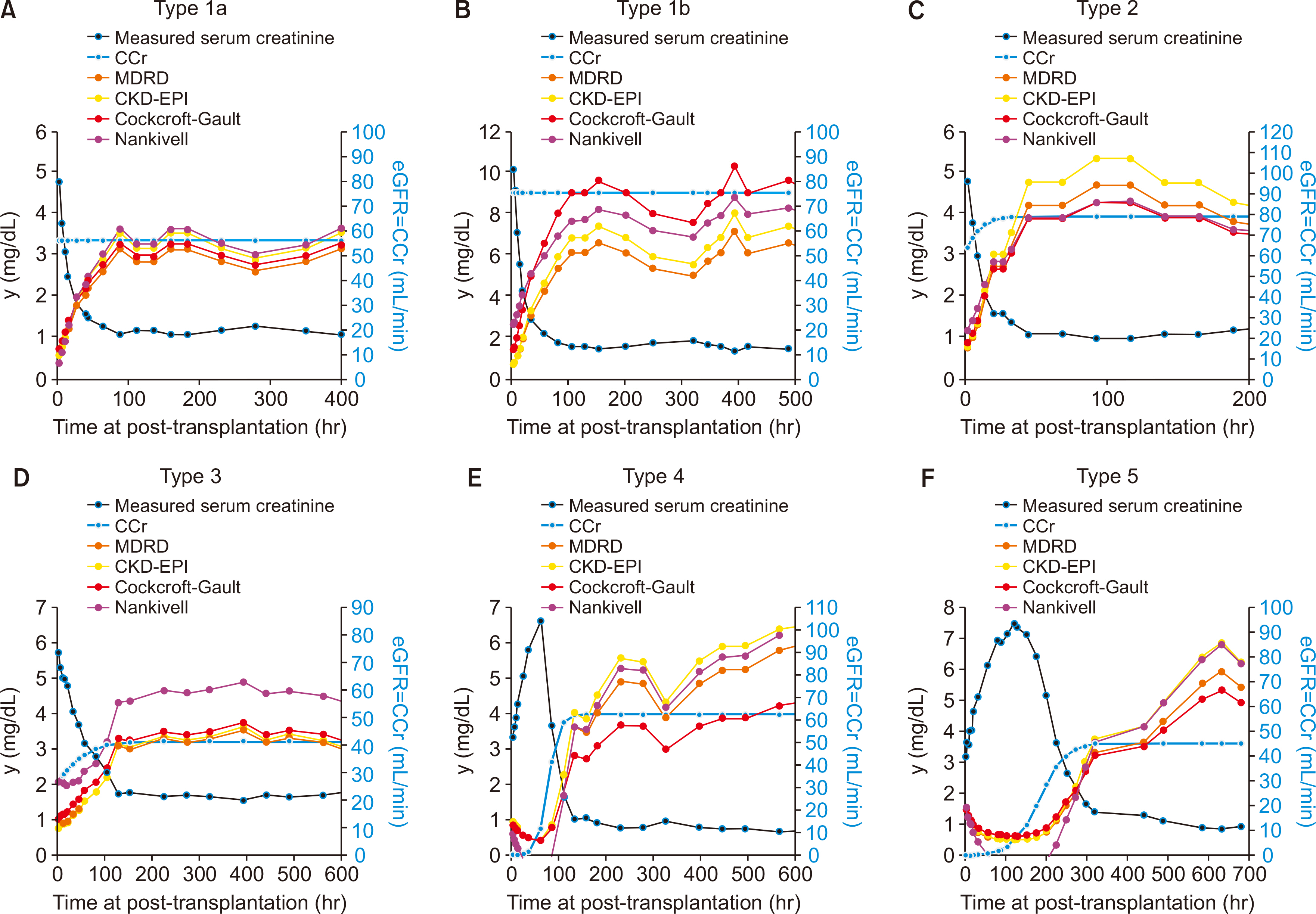
Commonly used equations for calculating estimated glomerular filtration rate (eGFR) are not applicable when serum creatinine (Scr) is rapidly changing like the post-transplant period. A new mathematical model applicable to the post-transplant period is required.
Methods
All 623 patients who underwent kidney transplantation from January 2008 to June 2018 at a single institute were included to validate the Scr mathematical equations, and 14,360 Scr laboratory results from the time of re-perfusion to 30 days post-transplantation were analyzed.
Results
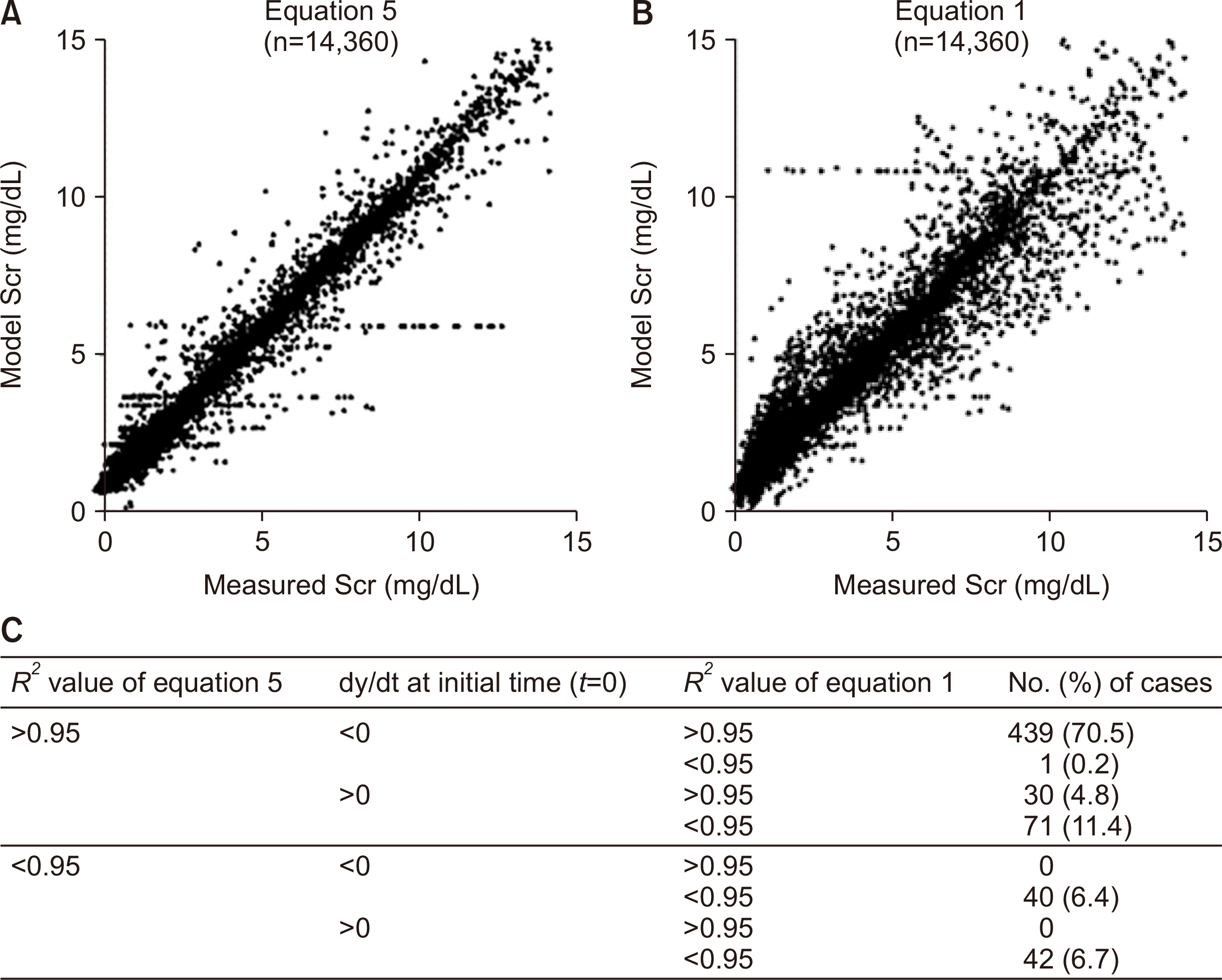
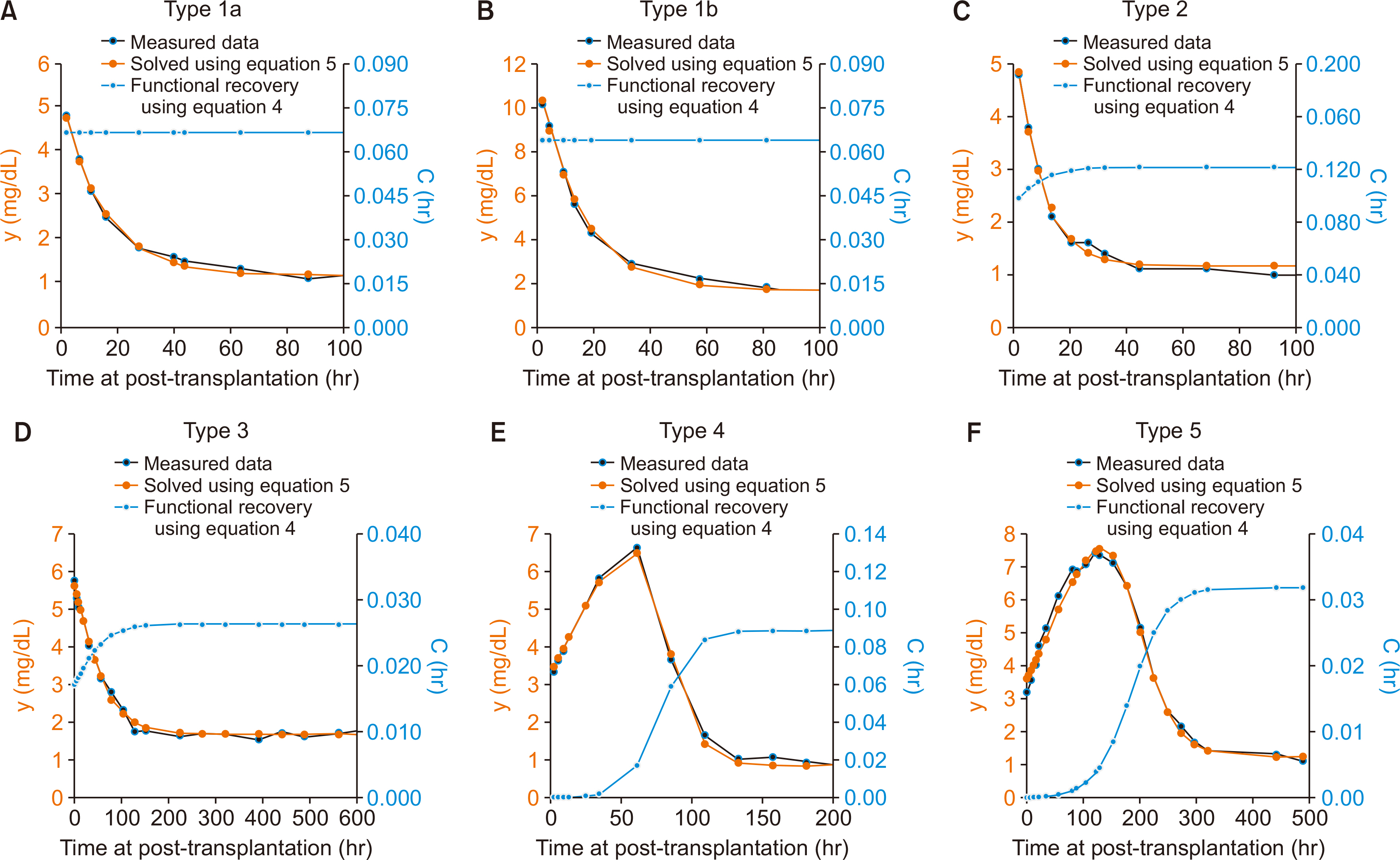
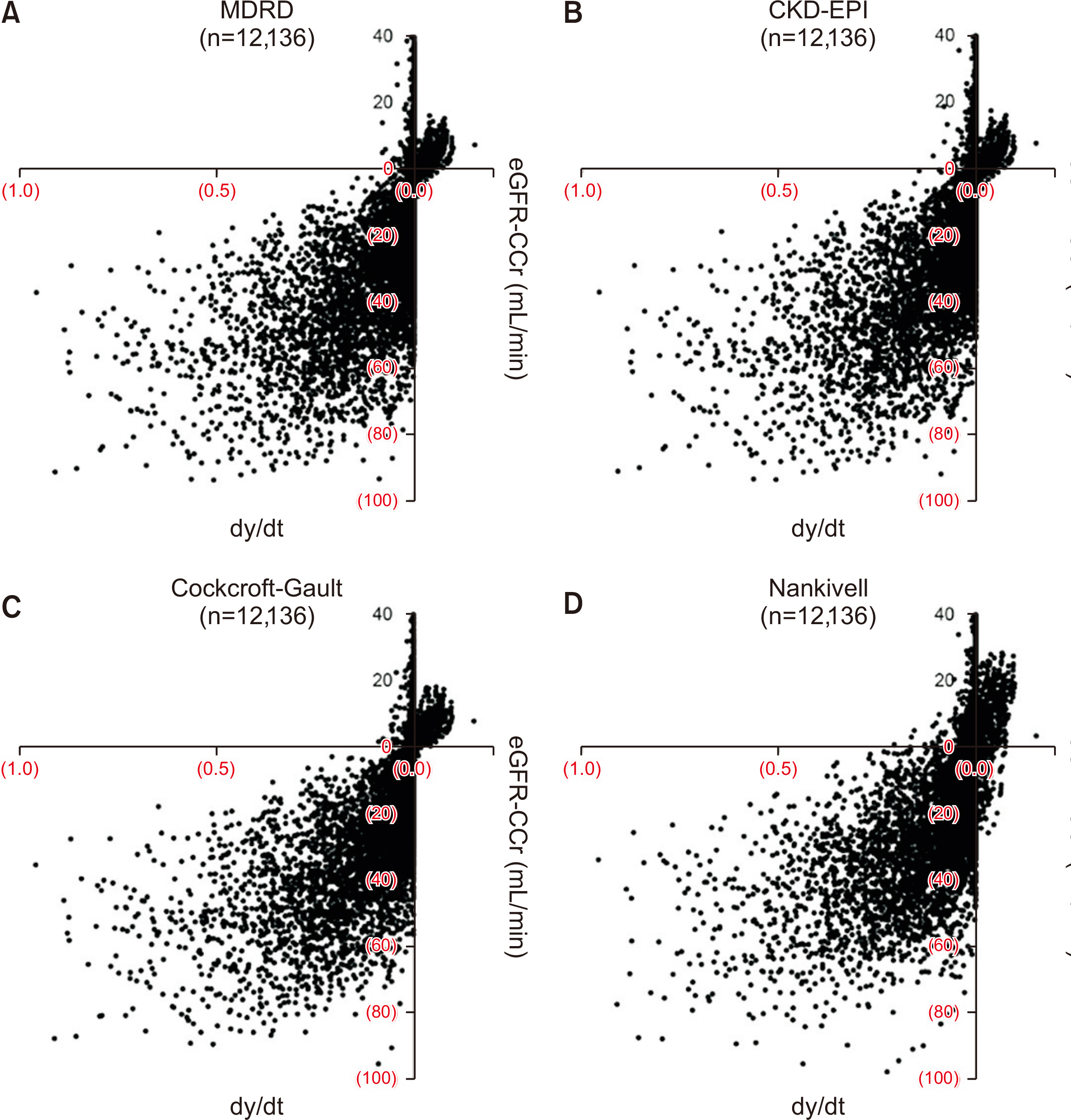
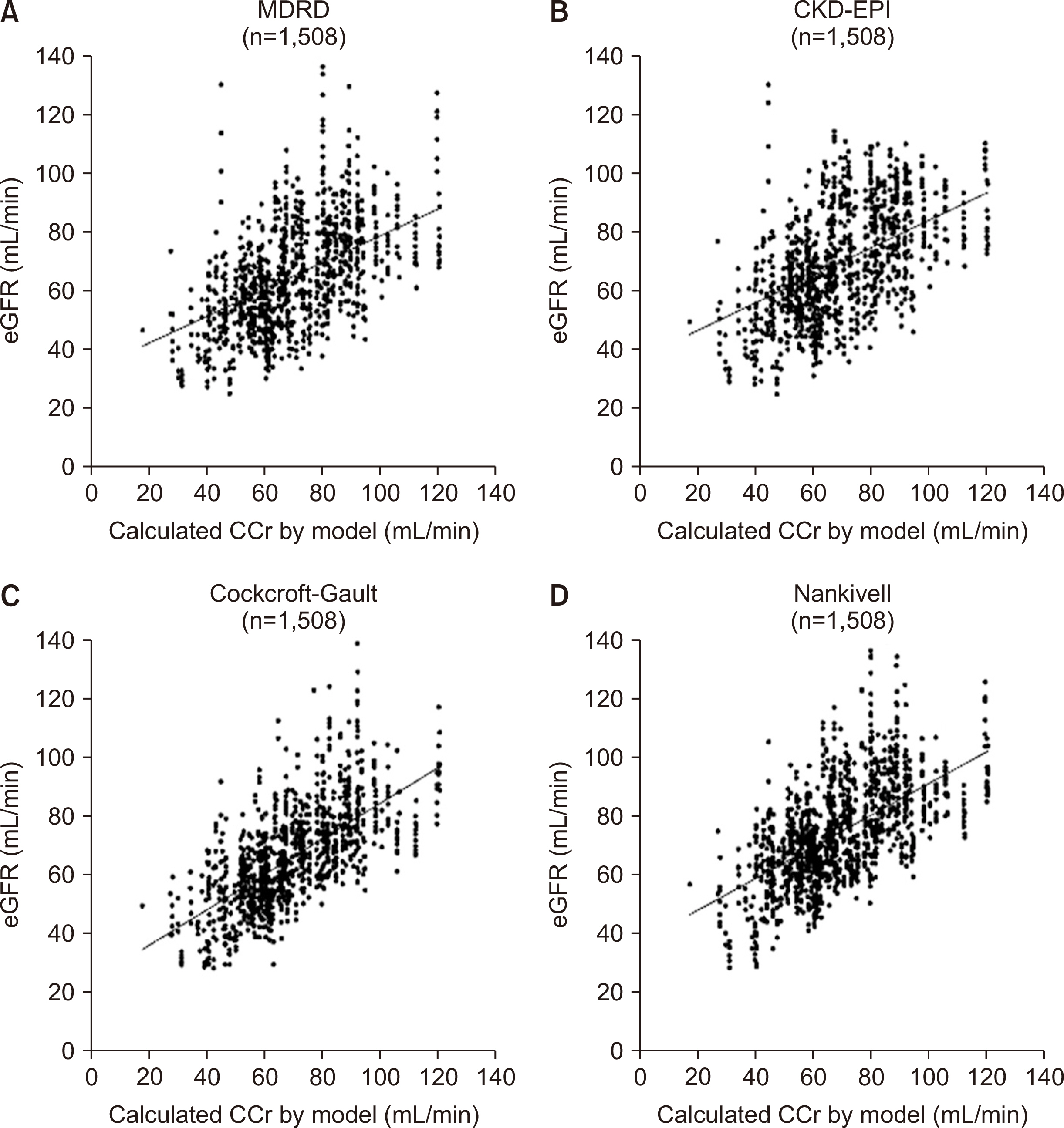
In the validation of model equations, linear regression analysis yielded adjusted R 2 values of 0.972 and 0.925 for equation 5 (applicable when renal function is changing) and equation 1 (applicable when renal function is unchanged), respectively. In selected cases, the population comprised individuals who presented an adjusted R 2 value >0.95 with equation 5. Linear regression analysis showed that adjusted R 2 values and Pearson's correlation coefficients for equation 5 and equation 1 were 0.994 and 0.997 (P<0.001) and 0.956 and 0.978 (P<0.001), respectively. Most of the eGFR formulas are mathematically applicable only if the creatinine input rate equals the creatinine output rate when comparing between commonly used eGFRs and creatinine clearance using the modeled equation.
Conclusions
The proposed equations can provide a new perspective for calculating renal function during the early phase of kidney transplantation. A study of a correlation between the equations and long-term graft outcomes is required.

Keyword

Creatinine; Kidney transplantation; Recovery of function; Mathematics

Figure

• 

  Fig. 1 Validation of model equations for serum creatinine (Scr) in total population. (A) Distribution of measured Scr values for the total population (n=623) and values obtained using equation 5 m(ertr+at+k5)v(ert+a). The R2 value is 0.972, and F-test value is 504,146.461 (P<0.001). (B) Distribution of measured Scr values for the total population (n=623) and values obtained using equation 1 mvc{1+e-c(t+k1)}. The R2 value is 0.925, and F-test value is 176,290.156 (P<0.001). (C) Fitness characteristics of the model equations for the total population (n=623). For each equation, good curve fit to the measured Scr values is defined as an adjusted R2 value greater than 0.95. Among the 541 (86.9%) cases that showed good fit with equation 5, the initial dydt values of 101 cases (18.7%) are greater than 0. Among the 101 cases with initial dydt>0, 71 cases (70.3%) showed poor fit with equation 1. None of the cases that showed poor fit with equation 5 showed good fit with equation 1. Equation 5 for improving renal function is more generalized and more applicable than equation 1 for stable renal function.

• 

  Fig. 2 Classification of the severity of pretransplant renal injury and recovery time at post-transplantation. (A) Example of type 1a. r=0.066472 (/hr), a=0.000000, k5=51.572055 (hr), m/v=0.077876 (mg/dL/hr). No pretransplant injury: 129 cases (23.8%). The constant “a” in equation 5 is nearly 0, and the constant “c” in equation 4 is equal to constant “r” in equation 5, which clinically suggests that the kidney graft reached full function immediately after reperfusion, and no further recovery of renal function was achieved after transplantation. (B) Example of type 1b. r=0.064122 (/hr), a=0.001416, k5=91.153870 (hr), m/v=0.106519 (mg/dL/hr). Minimal (1%) pretransplant injury: 29 cases (5.4%). The proportion of pre-transplant renal injury to expected full function of the graft, (r-C(0)r=a1+a), is less than 1%. (C) Example of type 2. r=0.121604 (/hr), a=0.293297, k5=41.148330 (hr), m/v=0.140837 (mg/dL/hr). Moderate (1%–50%) pretransplant injury and rapid functional recovery: 88 cases (16.3%). 0.01<(r-C(0)r=a1+a)≤0.5, and the recovery time required to reach 99% of the expected full function (functional capacity), t=In(99a)r based on equation 4, is less than 36 hours. (D) Example of type 3. r=0.026282 (/hr), a=0.591045, k5=170.169239 (hr), m/v=0.043779 (mg/dL/hr). Moderate (1%–50%) pretransplant injury and slow functional recovery: 90 cases (16.6%). 0.0150%) pretransplant injury and rapid functional recovery: 103 cases (19.0%). r-C(0)r=a1+a> 0.5, t=In(99a)r<144 hours (6 days). (F) Example of type 5. r=0.031957 (/hr), a=354.134151, k5=32,054.956071 (hr), m/v=0.039461 (mg/dL/hr). Severe (>50%) pretransplant injury slow functional recovery: 102 cases (18.9%). r-C(0)r=a1+a>0.5, t=In(99a)r≥144 hours (6 days).

• 

  Fig. 3 Comparison of estimated glomerular filtration rates (eGFRs) and modeled creatinine clearance (CCr) for the example case of different types. (A) Comparison of eGFRs and modeled CCr for type 1a case. r=0.066472 (/hr), a=0.000000. (B) Comparison of eGFRs and modeled CCr for type 1b case. r=0.064122 (/hr), a=0.001416. (C) Comparison of eGFRs and modeled CCr for type 2 case. r=0.121604 (/hr), a=0.293297. (D) Comparison of eGFRs and modeled CCr for type 3 case. r=0.026282 (/hr), a=0.591045. (E) Comparison of eGFRs and modeled CCr for type 4 case. r=0.088510 (/hr), a=983.131123. (F) Comparison of eGFRs and modeled CCr for type 5 case. r=0.031957 (/hr), a=354.134151. MDRD, modification of diet in renal disease; CKD-EPI, chronic kidney disease-epidemiology collaboration.

• 

  Fig. 4 Distribution of estimated glomerular filtration rate (eGFR)- creatinine clearance (CCr) as a function of dydt. (A) Scatter plot of modification of diet in renal disease (MDRD) eGFR-modeled CCr as a function of dydt. (B) Scatter plot of chronic kidney disease-epidemiology collaboration (CKD-EPI) eGFR-modeled CCr as a function of dydt. (C) Scatter plot of Cockcroft-Gault eGFR-modeled CCr as a function of dydt. (D) Scatter plot of Nankivell eGFR-modeled CCr as a function of dydt.

• 

  Fig. 5 Correlation between estimated glomerular filtration rate (eGFR) and modeled creatinine clearance (CCr) at dydt≒0. (A) Scatter plot of modification of diet in renal disease (MDRD) eGFR as a function of the CCr obtained with the model at –0.000000002

Reference

1. Cockcroft DW, Gault MH. 1976; Prediction of creatinine clearance from serum creatinine. Nephron. 16:31–41. DOI: 10.1159/000180580. PMID: 1244564.

2. Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D. 1999; A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med. 130:461–70. DOI: 10.7326/0003-4819-130-6-199903160-00002. PMID: 10075613. PMCID: PMC5223708.

3. Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF 3rd, Feldman HI, et al. 2009; A new equation to estimate glomerular filtration rate. Ann Intern Med. 150:604–12. DOI: 10.7326/0003-4819-150-9-200905050-00006. PMID: 19414839.

4. Nankivell BJ, Gruenewald SM, Allen RD, Chapman JR. 1995; Predicting glomerular filtration rate after kidney transplantation. Transplantation. 59:1683–9. DOI: 10.1097/00007890-199506270-00007. PMID: 7604438.

5. Delanaye P, Cavalier E, Cristol JP, Delanghe JR. 2014; Calibration and precision of serum creatinine and plasma cystatin C measurement: impact on the estimation of glomerular filtration rate. J Nephrol. 27:467–75. DOI: 10.1007/s40620-014-0087-7. PMID: 24711159.

6. Aitken E, Cooper C, Dempster N, McDermott M, Ceresa C, Kingsmore D. 2015; Delayed graft function is a syndrome rather than a diagnosis. Exp Clin Transplant. 13:19–25. PMID: 25654410.

7. Sharif A, Borrows R. 2013; Delayed graft function after kidney transplantation: the clinical perspective. Am J Kidney Dis. 62:150–8. DOI: 10.1053/j.ajkd.2012.11.050. PMID: 23391536. PMCID: PMC7504189.

8. Siedlecki A, Irish W, Brennan DC. 2011; Delayed graft function in the kidney transplant. Am J Transplant. 11:2279–96. DOI: 10.1111/j.1600-6143.2011.03754.x. PMID: 21929642.

9. Gregoir W. 1962; Congenital vesico-ureteral reflux. Acta Urol Belg. 30:286–300. PMID: 13901619.

10. Lich RJ, Howerton LW, Davis LA. 1961; Childhood urosepsis. J Ky Med Assoc. 59:1177–9. DOI: 10.1055/s-0040-1717072. PMID: 14465076.

11. Mitch WE, Walser M. 1978; A proposed mechanism for reduced creatinine excretion in severe chronic renal failure. Nephron. 21:248–54. DOI: 10.1159/000181400. PMID: 714198.

12. Levey AS, Eckardt KU, Tsukamoto Y, Levin A, Coresh J, Rossert J, et al. 2005; Definition and classification of chronic kidney disease: a position statement from Kidney Disease: Improving Global Outcomes (KDIGO). Kidney Int. 67:2089–100. DOI: 10.1111/j.1523-1755.2005.00365.x. PMID: 15882252.

13. White CA, Huang D, Akbari A, Garland J, Knoll GA. 2008; Performance of creatinine-based estimates of GFR in kidney transplant recipients: a systematic review. Am J Kidney Dis. 51:1005–15. DOI: 10.1053/j.ajkd.2008.02.308. PMID: 18455847.

14. Santos J, Martins LS. 2015; Estimating glomerular filtration rate in kidney transplantation: still searching for the best marker. World J Nephrol. 4:345–53. DOI: 10.5527/wjn.v4.i3.345. PMID: 26167457. PMCID: PMC4491924.

15. Schröppel B, Legendre C. 2014; Delayed kidney graft function: from mechanism to translation. Kidney Int. 86:251–8. DOI: 10.1038/ki.2014.18. PMID: 24522494. PMCID: PMC7477357.

16. Gaber AO, Mulgaonkar S, Kahan BD, Woodle ES, Alloway R, Bajjoka I, et al. 2011; YSPSL (rPSGL-Ig) for improvement of early renal allograft function: a double-blind, placebo-controlled, multi-center Phase IIa study. Clin Transplant. 25:523–33. DOI: 10.1111/j.1399-0012.2010.01295.x. PMID: 20573162.