J Korean Med Sci.  2020 Apr;35(18):e125. 10.3346/jkms.2020.35.e125.

Computed Tomography-Based Preoperative Simulation System for Pedicle Screw Fixation in Spinal Surgery

• Wi W
• Park SM
• Shin BS

• KMID: 2500218
• DOI: http://doi.org/10.3346/jkms.2020.35.e125

Abstract

Background
A preoperative planning system facilitates improving surgical outcomes that depend on the experience of the surgeons, thanks to real-time interaction between the system and surgeons. It visualizes intermediate surgical planning results to help surgeons discuss the planning. The purpose of this study was to demonstrate the use of a newly-developed preoperative planning system for surgeons less experienced in pedicle-screw fixation in spinal surgery, especially on patients with anatomical variations.
Methods
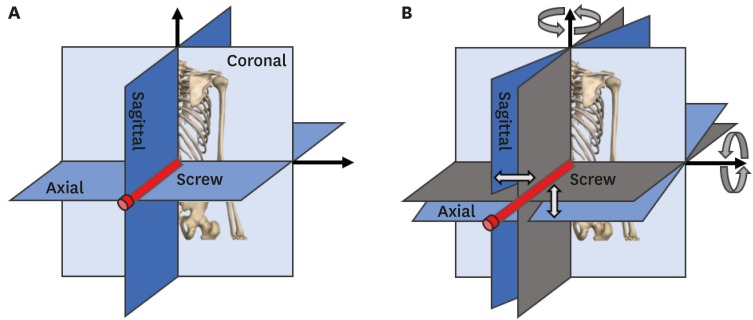
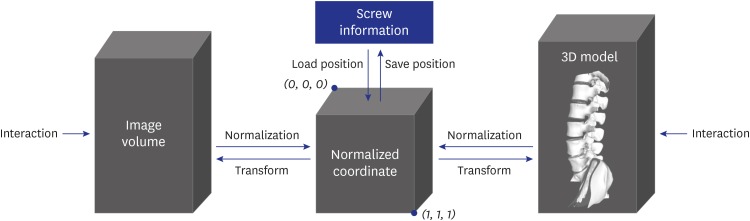
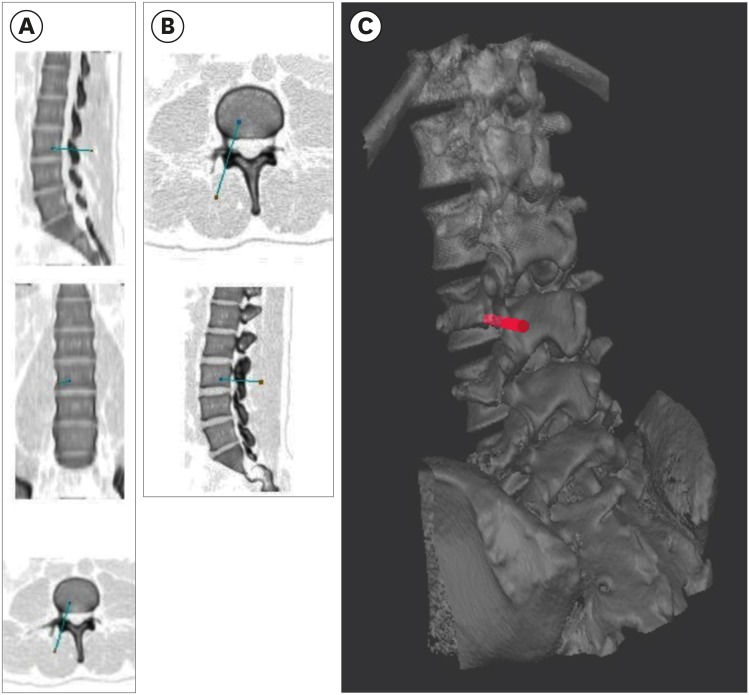
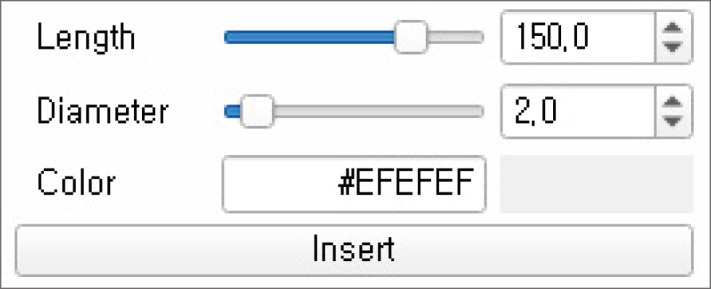
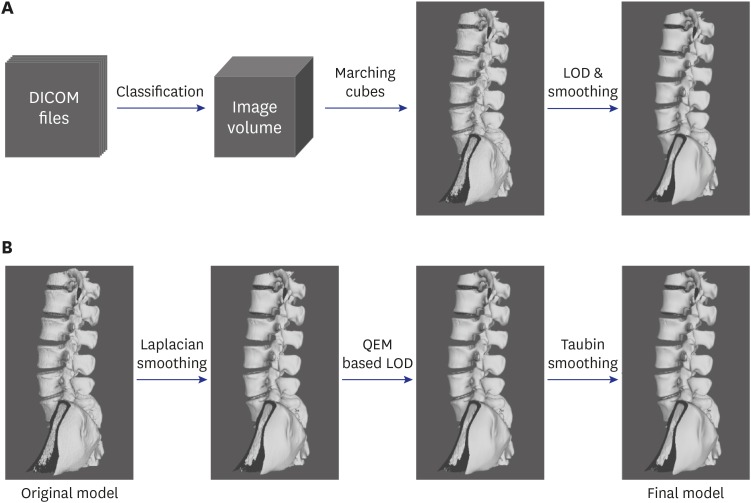
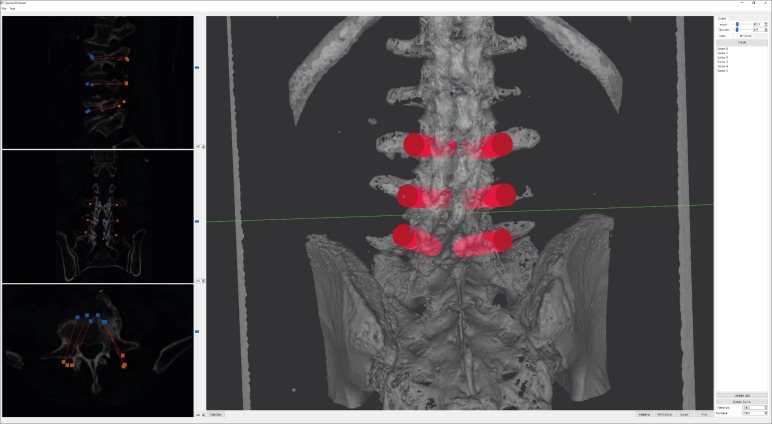
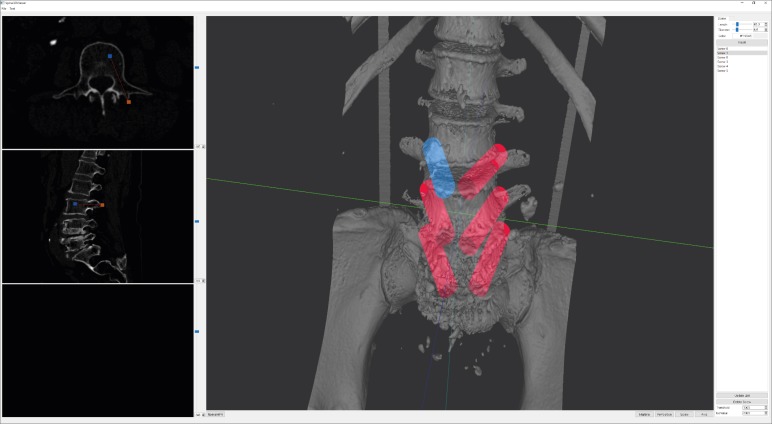
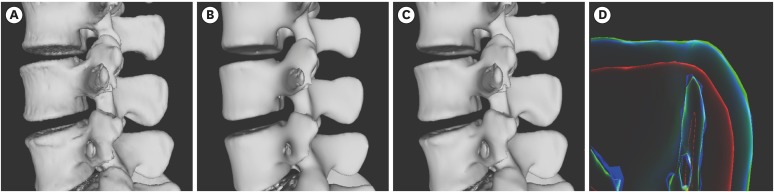
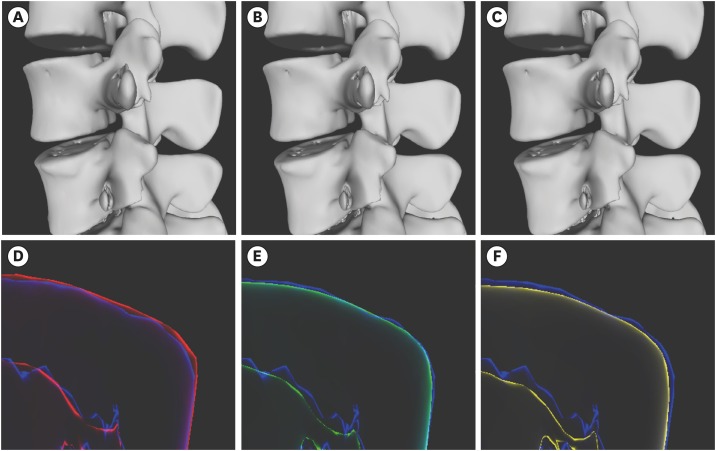
The marching cubes algorithm, a typical surface extraction technique, was applied to computed tomography (CT) images of vertebrae to enable three-dimensional (3D) reconstruction of a spinal mesh. Real-time processing of such data is difficult, as the surface mesh extracted from high-resolution CT data is rough, and the size of the mesh is large. To mitigate these factors, Laplacian smoothing was applied, followed by application of a quadric error metric-based mesh simplification to reduce the mesh size for the level-of-detail (LOD) image. Taubin smoothing was applied to smooth out the rough surface. On a multiplanar reconstruction (MPR) cross-sectional image or a 3D model view, the insertion position and orientation of the pedicle screw were manipulated using a mouse. The results after insertion were then visualized in each image.
Results
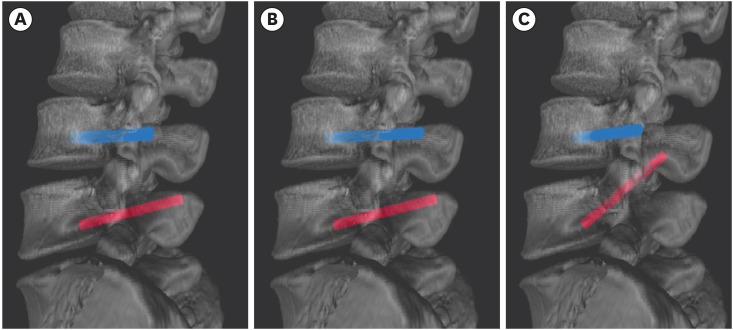
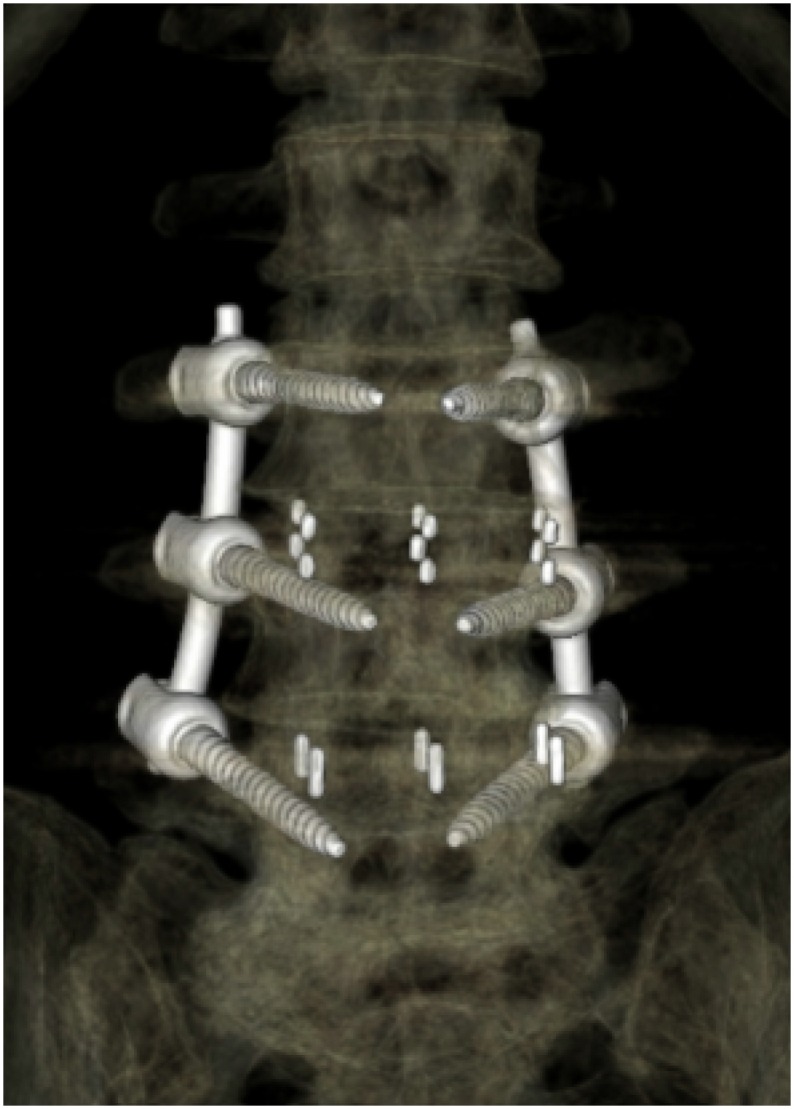
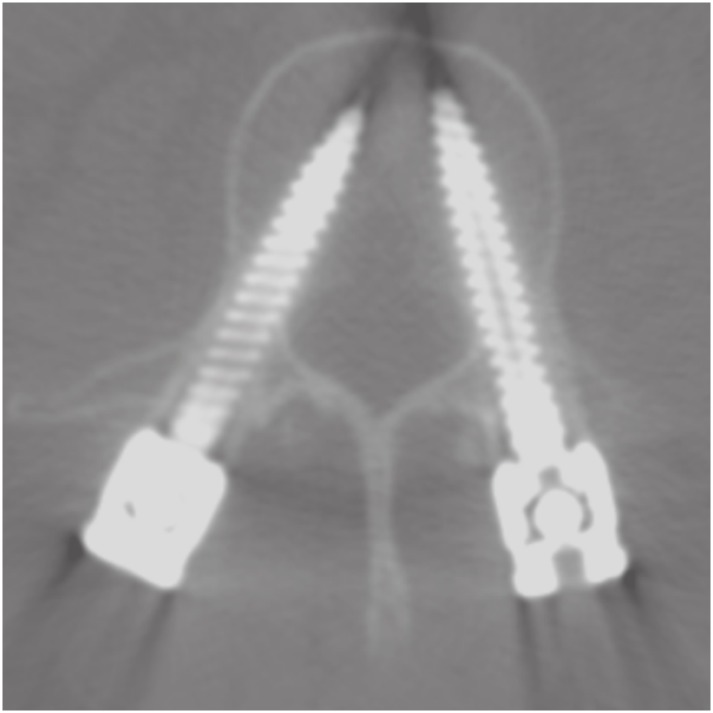
The system was used for pre-planning pedicle-screw fixation in spinal surgery. Using any pointing device such as a mouse, surgeons can manipulate the position and angle of the screws. The pedicle screws were easy to manipulate intuitively on the MPR images, and the accuracy of screw fixation was confirmed on a trajectory view and 3D images. After surgery, CT scans were performed again, and the CT images were checked to ensure that the screws were inserted properly.
Conclusion
The preoperative planning system allows surgeons and students who are not familiar with pedicle-screw fixation to safely undertake surgery following preoperative planning. It also provides opportunities for screw-fixation training and simulation.

Keyword

Surgical Planning; Pedicle-Screw Fixation; Spinal Surgery; Mesh Smoothing

Figure

• 

  Fig. 1 The constructions of the MPR and its trajectory. (A) MPR sections, (B) trajectory of the MPR sections.MPR = multiplanar reconstruction.

• 

  Fig. 2 The flow of preservation of coordinate consistency on the multiplanar reconstruction, trajectory of MPR, and 3D models using the normalized coordinate system.3D = three-dimensional.

• 

  Fig. 3 MPR, trajectory of MPR section views, and 3D-view screenshots on the simulator. (A) MPR section view with a screw inserted, (B) trajectory MPR section view, and (C) 3D model view. Colors of the captured MPR and trajectory MPR view images were reversed to improve visibility.MPR = multiplanar reconstruction, 3D = three-dimensional.

• 

  Fig. 4 Screw parameter correction dialog of the simulator providing options to change length, diameter, and color in the simulator.

• 

  Fig. 5 Comparison of screw models on 3D view with pedicle-screw correction in the simulator. (A) Screws with a length of 50 mm and diameter of 5 mm, (B) screws with a length of 65 mm and diameter of 4 mm, and (C) screws modified to different degrees on the 3D model view.3D = three-dimensional.

• 

  Fig. 6 3D model reconstruction and additional process in this study. (A) Overall process of 3D model reconstruction using DICOM format computed tomography images, (B) additional smoothing and LOD application process for the original model created using the marching cube algorithm.DICOM = digital imaging and communications in medicine, LOD = level-of-detail, QEM = quadric error metric, 3D = three-dimensional.

• 

  Fig. 7 A screenshot of screw-fixation planning on the multiplanar reconstruction section view.

• 

  Fig. 8 Correction of the pedicle-screw angle using the three-dimensional model view and the fixation position on the trajectory multiplanar reconstruction section view.

• 

  Fig. 9 Results of pedicle-screw fixation using external software.

• 

  Fig. 10 Computed tomography images taken to confirm the results after screw-fixation surgery.

• 

  Fig. 11 Visual comparison of LOD model and models of application of Laplacian and Taubin smoothing. (A) The LOD model, (B) the model that applied Laplacian smoothing in 8 iterations, (C) the model that applied Taubin smoothing in 30 iterations, (D) rendering image using x-ray shader for visual comparison of these models. The blue outline is the outline of (A), the red is (B) and the green is (C).LOD = level-of-detail.

• 

  Fig. 12 Visual comparison of results models according to the number of Laplacian and Taubin smoothing applications. (A), (B), and (C) are the models that received 4, 12, and 20 iterations of Laplacian smoothing and 50, 30, and 10 iterations of Taubin smoothing. (D), (E), and (F) are the rendering images using X-ray shader for visually comparing the model size changes according to the iterations of each smoothing algorithm applied. The blue outline is the level-of-detail model, as in Fig. 11A.

Reference

1. Park SM, Shen F, Kim HJ, Kim H, Chang BS, Lee CK, et al. How many screws are necessary to be considered an experienced surgeon for freehand placement of thoracolumbar pedicle screws?: analysis using the cumulative summation test for learning curve. World Neurosurg. 2018; 118:e550–6. PMID: 30257308.

2. Perna F, Borghi R, Pilla F, Stefanini N, Mazzotti A, Chehrassan M. Pedicle screw insertion techniques: an update and review of the literature. Musculoskelet Surg. 2016; 100(3):165–169. PMID: 27866324.

3. Esses SI, Sachs BL, Dreyzin V. Complications associated with the technique of pedicle screw fixation. A selected survey of ABS members. Spine. 1993; 18(15):2231–2238. PMID: 8278838.

4. 3D Slicer. https://www.slicer.org.

5. Song G, Bai H, Zhao Y, Han J, Liu X. Preoperative planning and simulation for pedicle screw insertion using computed tomography-based patient specific volume rendering combined with projection fluoroscopy. Int Robot Autom J. 2017; 2(1):25–29.

6. Xiang L, Zhou Y, Wang H, Zhang H, Song G, Zhao Y, et al. Significance of preoperative planning simulator for junior surgeons' training of pedicle screw insertion. J Spinal Disord Tech. 2015; 28(1):E25–E29. PMID: 25075987.

7. Yeom JS, Choy WS, Kim WJ, Kim HY, Kang JW, Kim YW, et al. A patient-specific surgical simulation system for spinal screw insertion composed of virtual roentgenogram, virtual C-arm, and rapid prototyping. J Korean Orthop Assoc. 2001; 36(2):161–166.

8. Park SK, Yeom JS, Won JH, Lee JC, Lee DH, Lee J, et al. C1-2 fixation using polyaxial screws and rods assisted by computer simulation for revision of failed posterior fusion: a technical report. J Korean Orthop Assoc. 2005; 40(6):778–781.

9. Eftekhar B, Ghodsi M, Ketabchi E, Rasaee S. Surgical simulation software for insertion of pedicle screws. Neurosurgery. 2002; 50(1):222–223. PMID: 11844256.

10. Muralidharan V, Swaminathan G, Devadhas D, Joseph BV. Patient-specific interactive software module for virtual preoperative planning and visualization of pedicle screw entry point and trajectories in spine surgery. Neurol India. 2018; 66(6):1766–1770. PMID: 30504578.

11. Klein S, Whyne CM, Rush R, Ginsberg HJ. CT-based patient-specific simulation software for pedicle screw insertion. J Spinal Disord Tech. 2009; 22(7):502–506. PMID: 20075813.

12. Rajon DA, Bolch WE. Marching cube algorithm: review and trilinear interpolation adaptation for image-based dosimetric models. Comput Med Imaging Graph. 2003; 27(5):411–435. PMID: 12821034.

13. Raj Ségonne F, Fischl B. Integration of topological constraints in medical image segmentation. In : Paragios N, Duncan J, Ayache N, editors. Handbook of Biomedical Imaging. Boston, MA: Springer;2015. p. 245–262.

14. Wang J, Yu Z. Feature-sensitive tetrahedral mesh generation with guaranteed quality. Comput Aided Des. 2012; 44(5):400–412. PMID: 22328787.

15. Zhang Y, Hughes TJ, Bajaj CL. An automatic 3D mesh generation method for domains with multiple materials. Comput Methods Appl Mech Eng. 2010; 199(5-8):405–415. PMID: 20161555.

16. Vollmer J, Mencl R, Müller H. Improved laplacian smoothing of noisy surface meshes. Comput Graph Forum. 1999; 18(3):131–138.

17. Manmadhachary A, Ravi Kumar Y, Krishnanand L. Improve the accuracy, surface smoothing and material adaption in STL file for RP medical models. J Manuf Process. 2016; 21:46–45.

18. Chartrand G, Cresson T, Chav R, Gotra A, Tang A, De Guise JA. Liver segmentation on CT and MR using Laplacian mesh optimization. IEEE Trans Biomed Eng. 2017; 64(9):2110–2121. PMID: 27893375.

19. Wang LC, Hung YC. Hole filling of triangular mesh segments using systematic grey prediction. Comput Aided Des. 2012; 44(12):1182–1189.

20. Sazonov I, Nithiarasu P. Semi-automatic surface and volume mesh generation for subject-specific biomedical geometries. Int J Numer Methods Biomed Eng. 2012; 28(1):133–157.

21. Jermyn M, Ghadyani H, Mastanduno MA, Turner W, Davis SC, Dehghani H, et al. Fast segmentation and high-quality three-dimensional volume mesh creation from medical images for diffuse optical tomography. J Biomed Opt. 2013; 18(8):86007. PMID: 23942632.

22. Kalaiselvi T, Sriramakrishnan P, Somasundaram K. Survey of using GPU CUDA programming model in medical image analysis. Inform Med Unlocked. 2017; 9:133–144.

23. Zhou K, Gong M, Huang X, Guo B. Data-parallel octrees for surface reconstruction. IEEE Trans Vis Comput Graph. 2011; 17(5):669–681. PMID: 20498507.

24. Garland M, Zhou Y. Quadric-based simplification in any dimension. ACM Trans Graph. 2005; 24(2):209–239.

25. Papageorgiou A, Platis N. Triangular mesh simplification on the GPU. Vis Comput. 2015; 31(2):235–244.

26. Matias van Kaick O, Pedrini H. A comparative evaluation of metrics for fast mesh simplification. Comput Graph Forum. 2006; 25(2):197–210.

27. Rypl D, Nerad J. Volume preserving smoothing of triangular isotropic three-dimensional surface meshes. Adv Eng Softw. 2016; 101:3–26.

28. Bian Z, Tong R. Feature-preserving mesh denoising based on vertices classification. Comput Aided Geom Des. 2011; 28(1):50–64.

29. Petitjean S. A survey of methods for recovering quadrics in triangle meshes. ACM Comput Surv. 2002; 34(2):211–262.

30. Gosselin MC, Neufeld E, Moser H, Huber E, Farcito S, Gerber L, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys Med Biol. 2014; 59(18):5287–5303. PMID: 25144615.

31. Deese K, Geilen M, Rieg R. A two-step smoothing algorithm for an automated product development process. Int J Simul Model. 2018; 17(2):308–317.

32. Chen CY, Cheng KY. A sharpness dependent filter for mesh smoothing. Comput Aided Geom Des. 2005; 22(5):76–391.

33. Gertzbein SD, Robbins SE. Accuracy of pedicular screw placement in vivo. Spine. 1990; 15(1):11–14. PMID: 2326693.

34. Tang M, Lee M, Kim YJ. Interactive Hausdorff distance computation for general polygonal models. ACM Trans Graph. 2009; 28(3):74.

35. Bonaretti S, Seiler C, Boichon C, Reyes M, Büchler P. Image-based vs. mesh-based statistical appearance models of the human femur: implications for finite element simulations. Med Eng Phys. 2014; 36(12):1626–1635. PMID: 25271191.