Healthc Inform Res.  2019 Jul;25(3):182-192. 10.4258/hir.2019.25.3.182.

Nature of Complex Network of Dengue Epidemic as a Scale-Free Network

• Malik HA
• Abid F
• Mahmood N
• Wahiddin M
• Malik A

• KMID: 2457470
• DOI: http://doi.org/10.4258/hir.2019.25.3.182

Abstract

OBJECTIVES
Dengue epidemic is a dynamic and complex phenomenon that has gained considerable attention due to its injurious effects. The focus of this study is to statically analyze the nature of the dengue epidemic network in terms of whether it follows the features of a scale-free network or a random network.
METHODS
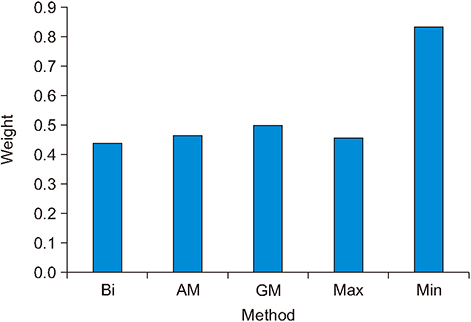
A multifarious network of Aedes aegypti is addressed keeping the viewpoint of a complex system and modelled as a network. The dengue network has been transformed into a one-mode network from a two-mode network by utilizing projection methods. Furthermore, three network features have been analyzed, the power-law, clustering coefficient, and network visualization. In addition, five methods have been applied to calculate the global clustering coefficient.
RESULTS
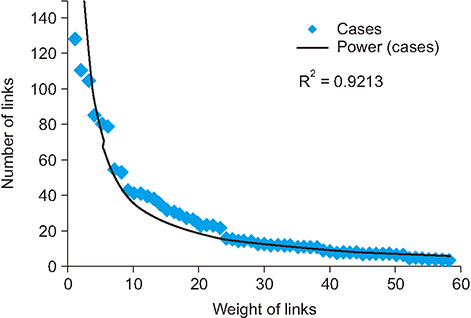
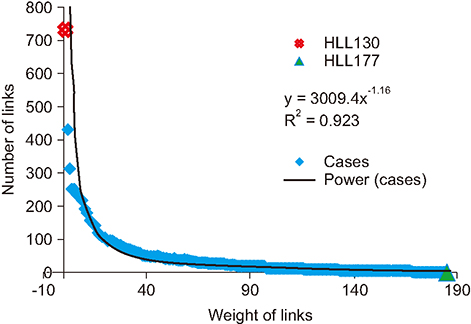
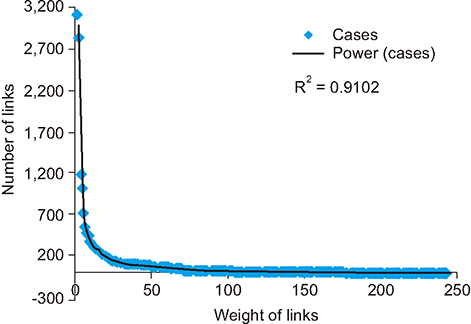
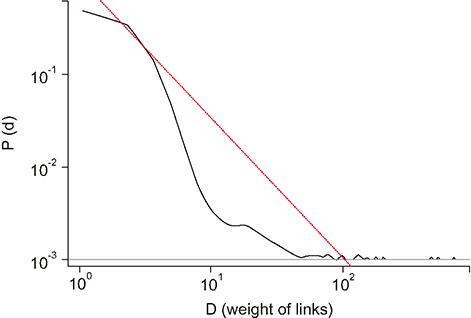
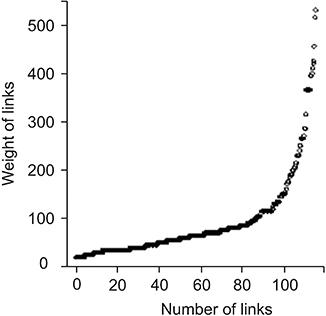
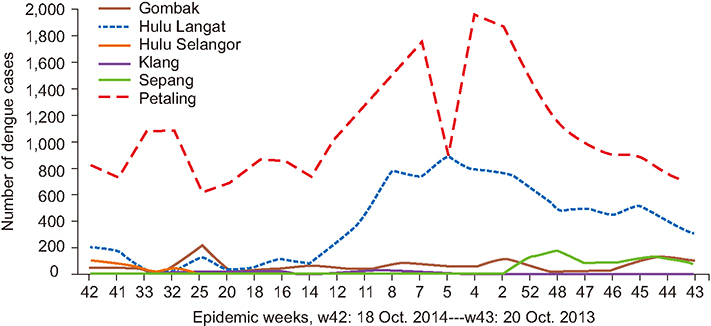
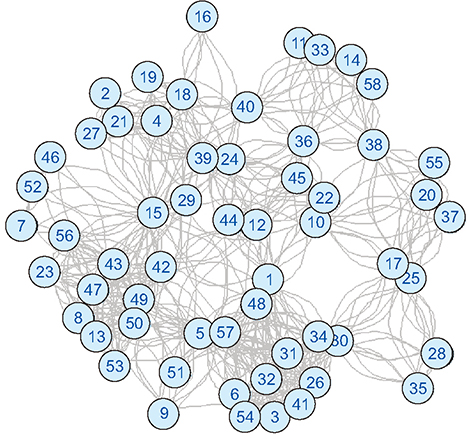
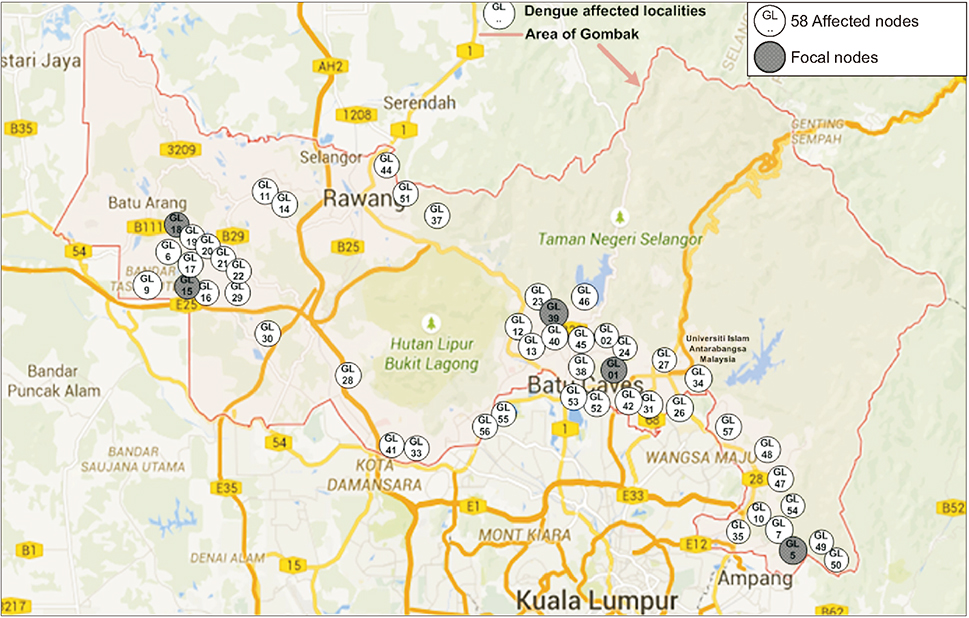
It has been observed that dengue epidemic follows a power-law, with the value of its exponent γ = −2.1. The value of the clustering coefficient is high for dengue cases, as weight of links. The minimum method showed the highest value among the methods used to calculate the coefficient. Network visualization showed the main areas. Moreover, the dengue situation did not remain the same throughout the observed period.
CONCLUSIONS
The results showed that the network topology exhibits the features of a scale-free network instead of a random network. Focal hubs are highlighted and the critical period is found. Outcomes are important for the researchers, health officials, and policy makers who deal with arbovirus epidemic diseases. Zika virus and Chikungunya virus can also be modelled and analyzed in this manner.

Keyword

Dengue Virus; Arboviruse; Epidemics; Big Data; Network Meta-Analysis

MeSH Terms

Administrative Personnel
Aedes
Arboviruses
Chikungunya virus
Critical Period (Psychology)
Dengue Virus
Dengue*
Humans
Methods
Zika Virus

Figure

• 

  Figure 1 Dengue cases in Gombak, Selangor (2013–2014).

• 

  Figure 2 Dengue cases in Hulu Langat, Selangor (2013–2014).

• 

  Figure 3 Dengue cases in Petaling, Selangor (2013–2014).

• 

  Figure 4 Probability distribution of node strength distribution on log scale in Selangor (2013–2014). The x-axis shows the strength of links and the y-axis shows the probability distribution of links strength.

• 

  Figure 5 Links density using weighted Newman method of projection.

• 

  Figure 6 Week-wis e comparison among six districts (October 20, 2013 to October 18, 2014).

• 

  Figure 7 Different methods of global clustering coefficients (comparison) in two-mode network. Bi: binary, AM: arithmetic mean, GM: geometric mean, Max: maximum, Min: minimum.

• 

  Figure 8 Graphical view of dengue network in Gombak.

• 

  Figure 9 Real map of Gombak, Malaysia. The map showed dengue affected noedes (GL is Gombak, location no. 1 to 58), image captured from Google maps and modified.

Reference

1. Newman ME. The structure of scientific collaboration networks. Proc Natl Acad Sci U S A. 2001; 98(2):404–409.

2. Malik HA, Mahmood N, Usman MH, Rziwan K, Abid F. Analysis of airport network in Pakistan utilizing complex network approach. Int J Adv Comput Sci Appl. 2019; 10(1):404–410.

3. Malik HA, Mahmood N, Usman MH, Abid F. Unweighted network study of Pakistani airports. In : Proceedings of 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET); 2019 Jan 30–31; Sukkur, Pakistan. p. 1–6.

4. Malik HA, Abid F, Gilal AR, Raja AS. Use of cloud computing in Hajj crowed management and complex systems. In : Proceedings of 2017 4th IEEE International Conference on Engineering Technologies and Applied Sciences (ICETAS); 2017 Nov 29–Dec 1; Salmabad, Bahrain. p. 1–5.

5. Malik HA, Mahesar AW, Abid F, Wahiddin MR. Two-mode complex network modeling of dengue epidemic in Selangor, Malaysia. In : Proceedings of the 5th International Conference on Information and Communication Technology for the Muslim World (ICT4M); 2014 Nov 17–18; Kuching, Malaysia. p. 1–6.

6. Kim PS, Lee PP, Levy D. Basic principles in modeling adaptive regulation and immunodominance. In : Ledzewicz U, editor. Mathematical methods and models in biomedicine. New York (NY): Springer Science & Business Media;2013. p. 33–57.

7. Malik HA, Abid F, Wahiddin MR, Bhatti Z. Robustness of dengue complex network under targeted versus random attack. Complexity. 2017; 2017:2515928.

8. Barabasi AL, Bonabeau E. Scale-free networks. Sci Am. 2003; 288(5):60–69.

9. Pastor-Satorras R, Vazquez A, Vespignani A. Dynamical and correlation properties of the internet. Phys Rev Lett. 2001; 87(25):258701.

10. Massad E, Ma S, Chen M, Struchiner CJ, Stollenwerk N, Aguiar M. Scale-free network of a dengue epidemic. Appl Math Comput. 2008; 195(2):376–381.

11. Malik HA, Mahesar AW, Abid F, Waqas A, Wahiddin MR. Two-mode network modeling and analysis of dengue epidemic behavior in Gombak, Malaysia. Appl Math Model. 2017; 43:207–220.

12. Uddin S, Murshed ST, Hossain L. Power-law behavior in complex organizational communication networks during crisis. Physica A Stat Mech Appl. 2011; 390(15):2845–2853.

13. Soewono E, Supriatna AK. A two-dimensional model for the transmission of dengue fever disease. Bull Malaysian Math Sci Soc. 2001; 24(1):49–97.

14. Pessanha JE. Risk assessment and risk maps using a simple dengue fever model. Dengue Bull. 2012; 36:73–86.

15. Ximenes R, Massad E. Modelling the risk of dengue for tourists in Rio de Janeiro during the FIFA confederation cup in Brazil 2013 [Internet]. Sao Paulo, Brazil: University of Sao Paulo;2013. cited at 2019 Jul 1. Available from: https://www.fields.utoronto.ca/programs/scientific/13-14/BIOMAT/presentations/Ximenes.pdf.

16. Coutinho FA, Burattini MN, Lopez LF, Massad E. Threshold conditions for a non-autonomous epidemic system describing the population dynamics of dengue. Bull Math Biol. 2006; 68(8):2263–2282.

17. Malik H, Waqas A, Abid F, Gilal A, Mahessar A, Koondar Y. Complex network of dengue epidemic and link prediction. Sindh Univ Res J (Sci Ser). 2016; 48(4):845–848.

18. Massad E, Ma S, Chen M, Struchiner CJ, Stollenwerk N, Aguiar M. Scale-free network of a dengue epidemic. Appl Math Comput. 2008; 195(2):376–381.

19. National Environment Agency. UNITEDengue crossborder data sharing provided countries with timely risk alerts [Internet]. Putrajaya, Malaysia: Ministry of Health;2014. cited at 2019 Jul 1. Available from: http://www.moh.gov.my/index.php/database_stores/attach_download/337/573.

20. Ministry of Health. Malaysia health systems research (Volume 1. Contextual analysis of the Malaysia health system) [Internet]. Putrajaya, Malaysia: Ministry of Health;2016. cited at 2019 Jul 1. Available from: http://www.moh.gov.my/moh/resources/Vol_1_MHSR_Contextual_Analysis_2016.pdf.

21. World Health Organization. Dengue and severe dengue [Internet]. Geneva, Switzerland: World Health Organization;c2019. cited at 2019 Jul 1. Available from: https://www.who.int/en/news-room/fact-sheets/detail/dengue-and-severe-dengue.

22. Ministry of Health Malaysia. Situasi Demam Denggi di Malaysia Bagi Minggu 2/2014 [Internet]. Putrajaya, Malaysia: Ministry of Health;c2019. cited at 2019 Jul 1. Available from: http://www.moh.gov.my/index.php/database_stores/store_view_page/17/465.

23. World Health Organization. Dengue Situation Update Number 441 [Internet]. Manila, Philippines: Regional Office for the Western Pacific Region, World Health Organization;2014. cited at 2019 Jul 1. Available from: https://reliefweb.int/sites/reliefweb.int/files/resources/dengue.biweekly.15jul2014.pdf.

24. Moheeput K, Goorah SS, Ramchurn SK. Spreading dynamics of a viral infection in a complex network. Int J Med Health Biomed Bioeng Pharm Eng. 2013; 7(7):373–377.

25. Side S, Noorani MS. A SIR model for spread of dengue fever disease (simulation for South Sulawesi, Indonesia and Selangor, Malaysia). World J Model Simul. 2013; 9(2):96–105.

26. Davis A, Gardner BB, Gardner MR. Deep south: a social anthropological study of caste and class. Columbia (SC): University of South Carolina Press;2009.

27. Barzel B, Barabasi AL. Universality in network dynamics. Nat Phys. 2013; 9:673–681.

28. Opsahl T. Triadic closure in two-mode networks: Redefining the global and local clustering coefficients. Soc Netw. 2013; 35(2):159–167.

29. Liljeros F, Edling CR, Amaral LA, Stanley HE, Aberg Y. The web of human sexual contacts. Nature. 2001; 411(6840):907–908.