Korean J Radiol.  2018 Oct;19(5):957-964. 10.3348/kjr.2018.19.5.957.

Contrast-Enhanced CT with Knowledge-Based Iterative Model Reconstruction for the Evaluation of Parotid Gland Tumors: A Feasibility Study

• Park CJ
• Kim KW
• Lee HJ
• Kim MJ
• Kim J

• KMID: 2418560
• DOI: http://doi.org/10.3348/kjr.2018.19.5.957

Abstract

OBJECTIVE
The purpose of this study was to determine the diagnostic utility of low-dose CT with knowledge-based iterative model reconstruction (IMR) for the evaluation of parotid gland tumors.
MATERIALS AND METHODS
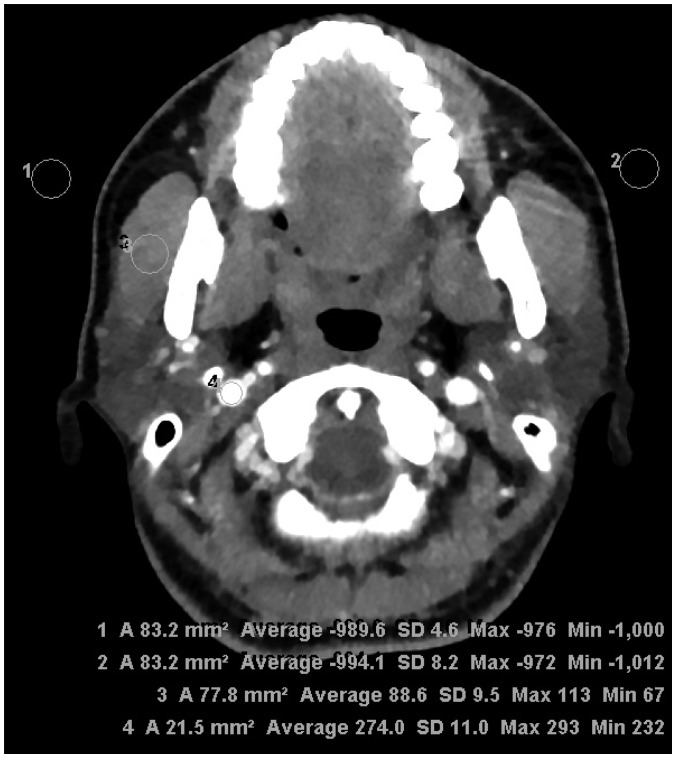
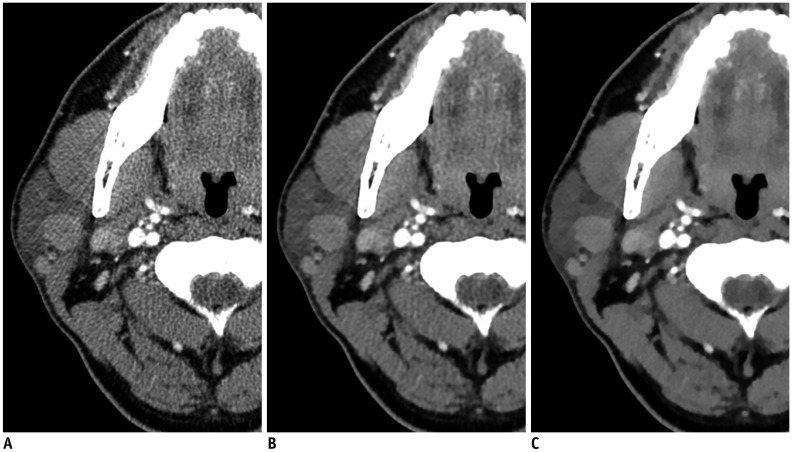
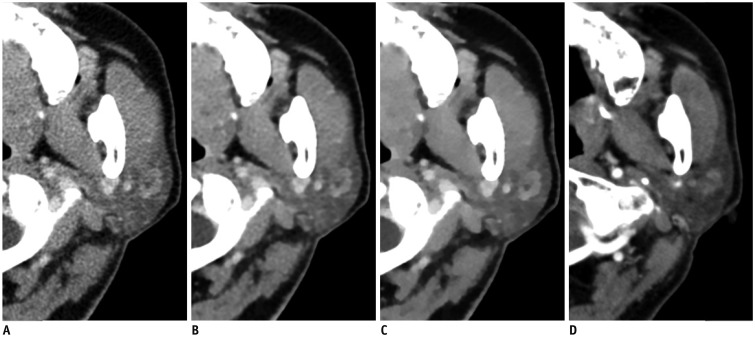
This prospective study included 42 consecutive patients who had undergone low-dose contrast-enhanced CT for the evaluation of suspected parotid gland tumors. Prior or subsequent non-low-dose CT scans within 12 months were available in 10 of the participants. Background noise (BN), signal-to-noise ratio (SNR), and contrast-to-noise ratio (CNR) were compared between non-low-dose CT images and images generated using filtered back projection (FBP), hybrid iterative reconstruction (iDose⁴; Philips Healthcare), and knowledge-based IMR. Subjective image quality was rated by two radiologists using five-point grading scales to assess the overall image quality, delineation of lesion contour, image sharpness, and noise.
RESULTS
With the IMR algorithm, background noise (IMR, 4.24 ± 3.77; iDose⁴, 8.77 ± 3.85; FBP, 11.73 ± 4.06; p = 0.037 [IMR vs. iDose⁴] and p < 0.001 [IMR vs. FBP]) was significantly lower and SNR (IMR, 23.93 ± 7.49; iDose⁴, 10.20 ± 3.29; FBP, 7.33 ± 2.03; p = 0.011 [IMR vs. iDose⁴] and p < 0.001 [IMR vs. FBP]) was significantly higher compared with the other two algorithms. The CNR was also significantly higher with the IMR compared with the FBP (25.76 ± 11.88 vs. 9.02 ± 3.18, p < 0.001). There was no significant difference in BN, SNR, and CNR between low-dose CT with the IMR algorithm and non-low-dose CT. Subjective image analysis revealed that IMR-generated low-dose CT images showed significantly better overall image quality and delineation of lesion contour with lesser noise, compared with those generated using FBP by both reviewers 1 and 2 (4 vs. 3; 4 vs. 3; and 3-4 vs. 2; p < 0.05 for all pairs), although there was no significant difference in subjective image quality scores between IMR-generated low-dose CT and non-low-dose CT images.
CONCLUSION
Iterative model reconstruction-generated low-dose CT is an alternative to standard non-low-dose CT without significantly affecting image quality for the evaluation of parotid gland tumors.

Keyword

Knowledge-based iterative reconstruction; Filtered back projection; Computed tomography; Parotid tumor; Parotid gland; Radiation dosage; Image reconstruction; Image quality

MeSH Terms

Feasibility Studies*
Humans
Image Processing, Computer-Assisted
Noise
Parotid Gland*
Prospective Studies
Radiation Dosage
Signal-To-Noise Ratio
Tomography, X-Ray Computed*
Weights and Measures

Figure

• 

  Fig. 1 Assessment of objective image quality at parotid gland level.Regions of interest were drawn to bilaterally measure SD of air (background noise) and attenuation of masseter muscle and internal jugular vein for estimation of signal-to-noise ratio and contrast-to-noise ratio. SD = standard deviation

• 

  Fig. 2 63-year-old woman with right parotid gland mass.Three axial image sets reconstructed using FBP (A), iDose4 (B), and IMR (C) algorithms. Compared with FBP- and iDose4-reconstructed images, significant decrease in streak artifacts related to dental amalgam was observed in parotid area with better conspicuity and definition of tumor margins in iterative model-reconstructed image. However, iterative model-reconstructed image showed relatively poor image sharpness, compared with FBP- and iDose4-reconstructed images. FBP = filtered back projection, iDose4 = hybrid iterative reconstruction, IMR = knowledge-based iterative model reconstruction

• 

  Fig. 3 68-year-old man with left parotid gland mass.Four axial image sets of low-dose CT reconstructed using FBP (A), iDose4 (B), and knowledge-based IMR (C) algorithms and non-low-dose CT (D). Compared with FBP- and iDose4-reconstructed images as well as non-low-dose CT, there is significant decrease in noise associated with parotid region and significantly better contrast and characterization of tumor in iterative model-reconstructed image. Parotid tissue appears blotchy and pixelated in iterative model-reconstructed image.

Reference

1. Lin CC, Tsai MH, Huang CC, Hua CH, Tseng HC, Huang ST. Parotid tumors: a 10-year experience. Am J Otolaryngol. 2008; 29:94–100. PMID: 18314019.

2. Barrett JF, Keat N. Artifacts in CT: recognition and avoidance. Radiographics. 2004; 24:1679–1691. PMID: 15537976.

3. Geyer LL, Schoepf UJ, Meinel FG, Nance JW Jr, Bastarrika G, Leipsic JA, et al. State of the art: iterative CT reconstruction techniques. Radiology. 2015; 276:339–357. PMID: 26203706.

4. Halpern EJ, Gingold EL, White H, Read K. Evaluation of coronary artery image quality with knowledge-based iterative model reconstruction. Acad Radiol. 2014; 21:805–811. PMID: 24809321.

5. Khawaja RDA, Singh S, Blake M, Harisinghani M, Choy G, Karaosmanoglu A, et al. Ultra-low dose abdominal MDCT: using a knowledge-based iterative model reconstruction technique for substantial dose reduction in a prospective clinical study. Eur J Radiol. 2015; 84:2–10. PMID: 25458225.

6. Park SB, Kim YS, Lee JB, Park HJ. Knowledge-based iterative model reconstruction (IMR) algorithm in ultralow-dose CT for evaluation of urolithiasis: evaluation of radiation dose reduction, image quality, and diagnostic performance. Abdom Imaging. 2015; 40:3137–3146. PMID: 26197735.

7. Ryu YJ, Choi YH, Cheon JE, Ha S, Kim WS, Kim IO. Knowledge-based iterative model reconstruction: comparative image quality and radiation dose with a pediatric computed tomography phantom. Pediatr Radiol. 2016; 46:303–315. PMID: 26546568.

8. Shrimpton PC, Hillier MC, Lewis MA, Dunn M. National survey of doses from CT in the UK: 2003. Br J Radiol. 2006; 79:968–980. PMID: 17213302.

9. Jessen KA, Panzer W, Shrimpton PC, Bongartz G, Gelejins J, Tosi G, et al. EUR 16262: European guidelines on quality criteria for computed tomography. Luxembourg: Office for Official Publications of the European Communities;2000.

10. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977; 33:159–174. PMID: 843571.

11. Hu Y, Pan S, Zhao X, Guo W, He M, Guo Q. Value and clinical application of orthopedic metal artifact reduction algorithm in CT scans after orthopedic metal implantation. Korean J Radiol. 2017; 18:526–535. PMID: 28458605.

12. Lim HJ, Chung MJ, Shin KE, Hwang HS, Lee KS. The impact of iterative reconstruction in low-dose computed tomography on the evaluation of diffuse interstitial lung disease. Korean J Radiol. 2016; 17:950–960. PMID: 27833411.

13. Choi DS, Na DG, Byun HS, Ko YH, Kim CK, Cho JM, et al. Salivary gland tumors: evaluation with two-phase helical CT. Radiology. 2000; 214:231–236. PMID: 10644130.

14. Shepp LA, Logan BF. The Fourier reconstruction of a head section. IEEE Trans Nucl Sci. 1974; 21:21–43.

15. Seibert JA. Iterative reconstruction: how it works, how to apply it. Pediatr Radiol. 2014; 44(Suppl 3):431–439. PMID: 25304701.

16. Hendrick RE. Breast MRI: fundamentals and technical aspects. New York, NY: Springer Science & Business Media;2007.

17. Yasaka K, Katsura M, Akahane M, Sato J, Matsuda I, Ohtomo K. Model-based iterative reconstruction for reduction of radiation dose in abdominopelvic CT: comparison to adaptive statistical iterative reconstruction. Springerplus. 2013; 2:209. PMID: 23687632.

18. Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol. 2008; 53:4777–4807. PMID: 18701771.

19. Qi H, Chen Z, Zhou L. CT image reconstruction from sparse projections using adaptive TpV regularization. Comput Math Methods Med. 2015; 2015:354869. PMID: 26089962.

20. Mehta D, Thompson R, Morton T, Dhanantwari A, Shefer E. Iterative model reconstruction: simultaneously lowered computed tomography radiation dose and improved image quality. Med Phys Int J. 2013; 2:147–155.

21. Boone JM. Determination of the presampled MTF in computed tomography. Med Phys. 2001; 28:356–360. PMID: 11318317.

22. Siewerdsen JH, Cunningham IA, Jaffray DA. A framework for noise-power spectrum analysis of multidimensional images. Med Phys. 2002; 29:2655–2671. PMID: 12462733.