J Adv Prosthodont.  2017 Aug;9(4):278-286. 10.4047/jap.2017.9.4.278.

Theoretical axial wall angulation for rotational resistance form in an experimental-fixed partial denture

• Bowley JF
• Kaye EK
• Garcia RI

• KMID: 2398075
• DOI: http://doi.org/10.4047/jap.2017.9.4.278

Abstract

PURPOSE
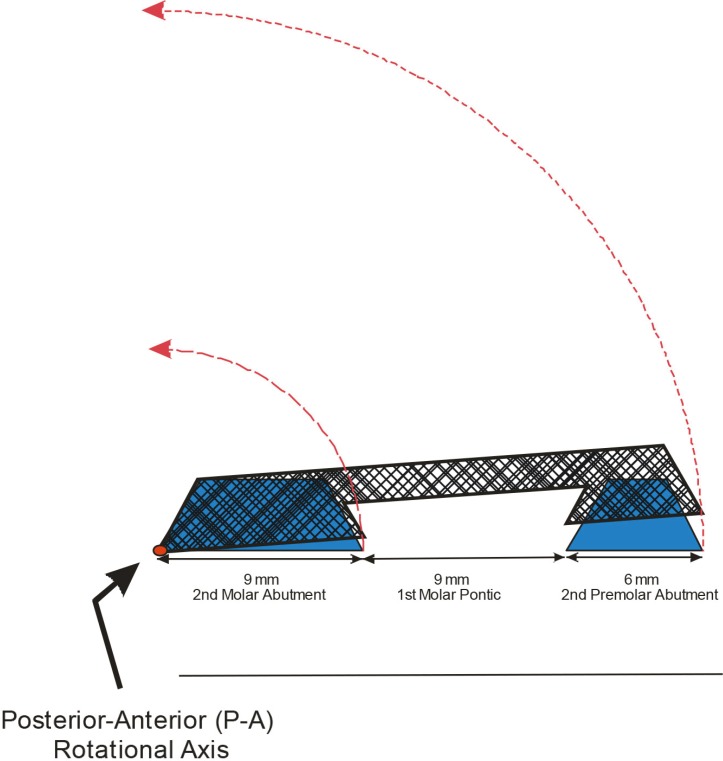
The aim of this study was to determine the influence of long base lengths of a fixed partial denture (FPD) to rotational resistance with variation of vertical wall angulation.
MATERIALS AND METHODS
Trigonometric calculations were done to determine the maximum wall angle needed to resist rotational displacement of an experimental-FPD model in 2-dimensional plane. The maximum wall angle calculation determines the greatest taper that resists rotation. Two different axes of rotation were used to test this model with five vertical abutment heights of 3-, 3.5-, 4-, 4.5-, and 5-mm. The two rotational axes were located on the mesial-side of the anterior abutment and the distal-side of the posterior abutment. Rotation of the FPD around the anterior axis was counter-clockwise, Posterior-Anterior (P-A) and clockwise, Anterior-Posterior (A-P) around the distal axis in the sagittal plane.
RESULTS
Low levels of vertical wall taper, ≤ 10-degrees, were needed to resist rotational displacement in all wall height categories; 2-to-6-degrees is generally considered ideal, with 7-to-10-degrees as favorable to the long axis of the abutment. Rotation around both axes demonstrated that two axial walls of the FPD resisted rotational displacement in each direction. In addition, uneven abutment height combinations required the lowest wall angulations to achieve resistance in this study.
CONCLUSION
The vertical height and angulation of FPD abutments, two rotational axes, and the long base lengths all play a role in FPD resistance form.

Keyword

Fixed partial denture; Resistance form

MeSH Terms

Denture, Partial*
Denture, Partial, Fixed

Figure

• 

  Fig. 1 Angle A illustrates Convergence Angle of two opposing walls of a tooth preparation.Angle BCD illustrates the single preparation Single Wall Angulation Specified in Rotational Resistance Form. Line BC represents the distal wall of tooth preparation. Line CD represents the long axis of the tooth (Line BC as distal wall resists rotation around an axis located on the opposite side of the preparation in a clock-wise rotational displacement). Arc F represents the distal margin of crown's rotational path around rotational axis E. The arc intersects incisal portion of preparation which represents resistance to rotational dislodgement (angles and arc NOT DRAWN TO SCALE, illustrative only).

• 

  Fig. 2 Illustration of simulated-FPD 2-D model.(A) 2nd premolar and 2nd molar abutments with B9-, 6-mm, H3-, 4-, 5-mm, (B) Simulated FPD with 2nd molar abutment, 1st molar pontic, and 2nd premolar abutment, (C) Both abutments with simulated FPD rotating around an P-A axis on mesial of 2nd premolar abutment.

• 

  Fig. 3 Illustration of A-P (Anterior-Posterior) Rotation Model with its axis on distal of 2nd molar abutment.

• 

  Fig. 4 (A) Illustration of simulated FPD even (black) P-A Rotation versus uneven (red), (B) Steps 1 & 2 in trigonometric calculations of change in hypotenuse (BTotal 24-mm) length with the change in axis of rotation to H5-mm to H3-mm (2nd Molar Abutment H5-mm).

• 

  Fig. 5 A-P (Anterior-Posterior) uneven abutment model with a rotational axis on distal 2nd molar abutment (H3-mm) with 2nd premolar abutment (H5-mm).

• 

  Fig. 6 Dependent variables, α1 and 3 & α2 and 4 of the simulated FPD-model as calculated with trigonometric equations shown below (2 of sides of Right Triangle with Pythagorean Theorem to calculate third side then calculation of angle(s) with Trigonometric formula):Maximal Wall Taper/Resistance FormEven Margin/Wall Heights α1 and 3 & Uneven Margin/Wall Heights α2 and 4Equation #1 (Fig. 6) α1 and 3 = ½[Arc Sin (H/B)] (angulation in °)Equation #2 Side ac of right triangle abc (Fig. 6) ac=ab2+bc2(mm)Equation #3 Side de of right triangle cde (Fig. 6) de=ce2+cd2(mm)Equation #4 Side ef of right triangle aef (Fig. 6) ef = df - de (mm)Equation #5 Maximal Uneven Abutment Wall Taper (Fig. 6) α2 and 4 = Arc Tangent [(ef) ÷ (af)] (angulation in °)

Reference

1. The Glossary of prosthodontic terms. J Prosthet Dent. 2005; 94:10–92. PMID: 16080238.

2. Prothero JH. Prosthetetic dentistry. Chicago: Medico-Dental Publishing Co;1923. p. 1128.

3. Dykema RW, Goodacre CJ, Phillips RW. Johnston's modern practice in fixed prosthodontics. Philadelphia: Saunders;1986. p. 22–27.

4. Shillingburg HT, Jacobi R, Brackett SE. Fundamentals of tooth preparations for cast metal and porcelain restorations. Chicago: Quintessence;1987. p. 13–31.

5. Malone FP, Koth DL. Tylman's theory and practice of fixed prosthodontics. 8th ed. St. Louis: Ishiyaku EuroAmerica;1989. p. 113–143.

6. Rosenstiel SF, Land MF, Fuijimoto J. Contemporary fixed prosthodontics. 4th ed. St. Louis: Mosby;2006. p. 226–257.

7. Goodacre CJ, Campagni WV, Aquilino SA. Tooth preparations for complete crowns: an art form based on scientific principles. J Prosthet Dent. 2001; 85:363–376. PMID: 11319534.

8. Kaufman EG, Coelho DH, Colin L. Factors influencing the retention of cemented gold castings. J Prosthet Dent. 1961; 11:487–502.

9. Nicholls JI. Crown retention. Part I. Stress analysis of symmetric restorations. J Prosthet Dent. 1974; 31:179–184. PMID: 4520666.

10. Hegdahl T, Silness J. Preparation areas resisting displacement of artificial crowns. J Oral Rehabil. 1977; 4:201–207. PMID: 268415.

11. Woolsey GD, Matich JA. The effect of axial grooves on the resistance form of cast restorations. J Am Dent Assoc. 1978; 97:978–980. PMID: 363771.

12. Mack PJ. A theoretical and clinical investigation into the taper achieved on crown and inlay preparations. J Oral Rehabil. 1980; 7:255–265. PMID: 6995565.

13. Potts RG, Shillingburg HT Jr, Duncanson MG Jr. Retention and resistance of preparations for cast restorations. J Prosthet Dent. 1980; 43:303–308. PMID: 6986461.

14. Weed RM, Baez RJ. A method for determining adequate resistance form of complete cast crown preparations. J Prosthet Dent. 1984; 52:330–334. PMID: 6384470.

15. Dodge WW, Weed RM, Baez RJ, Buchanan RN. The effect of convergence angle on retention and resistance form. Quintessence Int. 1985; 16:191–194. PMID: 3887460.

16. Zuckerman GR. Factors that influence the mechanical retention of the complete crown. Int J Prosthodont. 1988; 1:196–200. PMID: 3074808.

17. Zuckerman GR. Resistance form for the complete veneer crown: principles of design and analysis. Int J Prosthodont. 1988; 1:302–307. PMID: 3075911.

18. Parker MH, Gunderson RB, Gardner FM, Calverley MJ. Quantitative determination of taper adequate to provide resistance form: concept of limiting taper. J Prosthet Dent. 1988; 59:281–288. PMID: 3279183.

19. Nordlander J, Weir D, Stoffer W, Ochi S. The taper of clinical preparations for fixed prosthodontics. J Prosthet Dent. 1988; 60:148–151. PMID: 3172001.

20. Zuckerman GR. Analysis of resistance and retention of complete veneer crown retainers. Quintessence Int. 1990; 21:629–635. PMID: 2094865.

21. Parker MH, Malone KH 3rd, Trier AC, Striano TS. Evaluation of resistance form for prepared teeth. J Prosthet Dent. 1991; 66:730–733. PMID: 1805019.

22. Parker MH, Calverley MJ, Gardner FM, Gunderson RB. New guidelines for preparation taper. J Prosthodont. 1993; 2:61–66. PMID: 8374714.

23. Kamposiora P, Papavasilious G, Bayne SC, Felton DA. Finite element analysis estimates of cement microfracture under complete veneer crowns. J Prosthet Dent. 1994; 71:435–441. PMID: 8006836.

24. Wiskott HW, Nicholls JI, Belser UC. The relationship between abutment taper and resistance of cemented crowns to dynamic loading. Int J Prosthodont. 1996; 9:117–139. PMID: 8639233.

25. Wiskott HW, Nicholls JI, Belser UC. The effect of tooth preparation height and diameter on the resistance of complete crowns to fatigue loading. Int J Prosthodont. 1997; 10:207–215. PMID: 9484051.

26. Augereau D, Renault P, Pierrisnard L, Barquins M. Three-dimensional finite element analysis of the retention of fixed partial dentures. Clin Oral Investig. 1997; 1:141–146.

27. Trier AC, Parker MH, Cameron SM, Brousseau JS. Evaluation of resistance form of dislodged crowns and retainers. J Prosthet Dent. 1998; 80:405–409. PMID: 9791785.

28. Wiskott HW, Krebs C, Scherrer SS, Botsis J, Belser UC. Compressive and tensile zones in the cement interface of full crowns: a technical note on the concept of resistance. J Prosthodont. 1999; 8:80–91. PMID: 10740506.

29. Zidan O, Ferguson GC. The retention of complete crowns prepared with three different tapers and luted with four different cements. J Prosthet Dent. 2003; 89:565–571. PMID: 12815350.

30. Proussaefs P, Campagni W, Bernal G, Goodacre C, Kim J. The effectiveness of auxiliary features on a tooth preparation with inadequate resistance form. J Prosthet Dent. 2004; 91:33–41. PMID: 14739891.

31. Parker MH. Resistance form in tooth preparation. Dent Clin North Am. 2004; 48:387–396.

32. Bowley JF, Sun AF, Barouch KK. Effect of margin location on crown preparation resistance form. J Prosthet Dent. 2004; 92:546–550. PMID: 15583560.

33. Cameron SM, Morris WJ, Keesee SM, Barsky TB, Parker MH. The effect of preparation taper on the retention of cemented cast crowns under lateral fatigue loading. J Prosthet Dent. 2006; 95:456–461. PMID: 16765159.

34. Bowley JF, Kieser J. Axial-wall inclination angle and vertical height interactions in molar full crown preparations. J Dent. 2007; 35:117–123. PMID: 16911851.

35. Bowley JF, Lai WF. Surface area improvement with grooves and boxes in mandibular molar crown preparations. J Prosthet Dent. 2007; 98:436–444. PMID: 18061737.

36. Bowley JF, Ichim IP, Kieser JA, Swain MV. FEA evaluation of the resistance form of a premolar crown. J Prosthodont. 2013; 22:304–312. PMID: 23279111.

37. Lial ML, Schneider DI, Hornsby EJ. College algebra and trigonometry. New York: ddison-Wesley;2004. p. 472–531.