Investig Magn Reson Imaging.  2016 Dec;20(4):215-223. 10.13104/imri.2016.20.4.215.

Image Denoising for Metal MRI Exploiting Sparsity and Low Rank Priors

• Choi S
• Park JS
• Kim H
• Park J

• KMID: 2366403
• DOI: http://doi.org/10.13104/imri.2016.20.4.215

Abstract

PURPOSE
The management of metal-induced field inhomogeneities is one of the major concerns of distortion-free magnetic resonance images near metallic implants. The recently proposed method called "Slice Encoding for Metal Artifact Correction (SEMAC)" is an effective spin echo pulse sequence of magnetic resonance imaging (MRI) near metallic implants. However, as SEMAC uses the noisy resolved data elements, SEMAC images can have a major problem for improving the signal-to-noise ratio (SNR) without compromising the correction of metal artifacts. To address that issue, this paper presents a novel reconstruction technique for providing an improvement of the SNR in SEMAC images without sacrificing the correction of metal artifacts.
MATERIALS AND METHODS
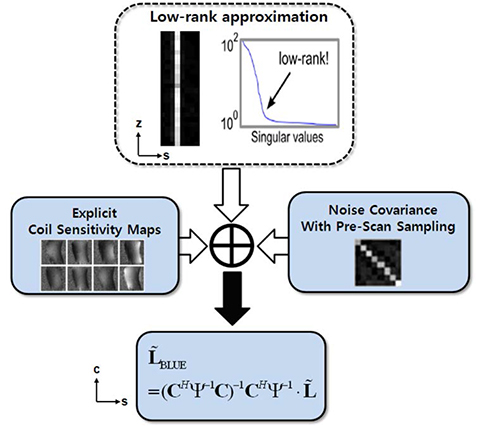
Low-rank approximation in each coil image is first performed to suppress the noise in the slice direction, because the signal is highly correlated between SEMAC-encoded slices. Secondly, SEMAC images are reconstructed by the best linear unbiased estimator (BLUE), also known as Gauss-Markov or weighted least squares. Noise levels and correlation in the receiver channels are considered for the sake of SNR optimization. To this end, since distorted excitation profiles are sparse, l1 minimization performs well in recovering the sparse distorted excitation profiles and the sparse modeling of our approach offers excellent correction of metal-induced distortions.
RESULTS
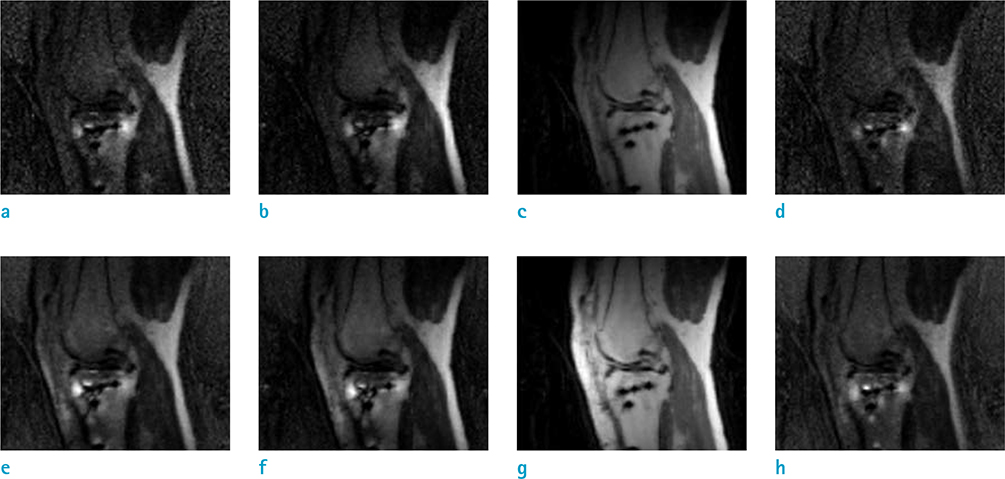
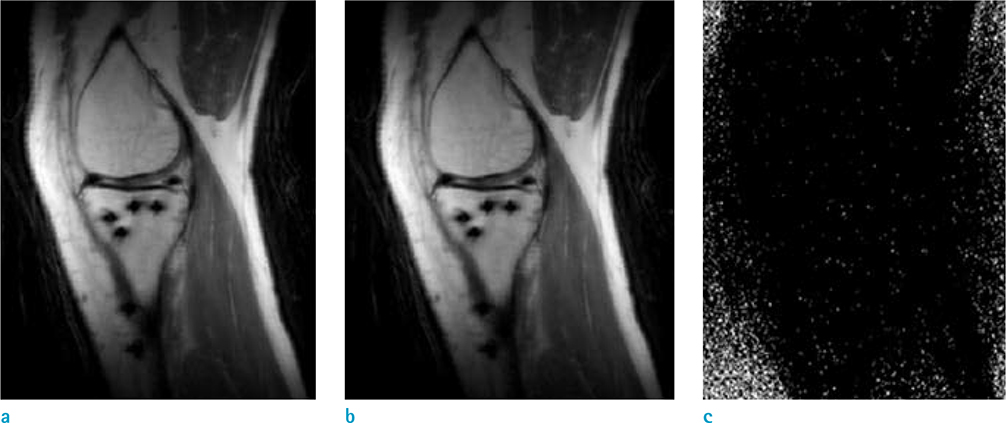
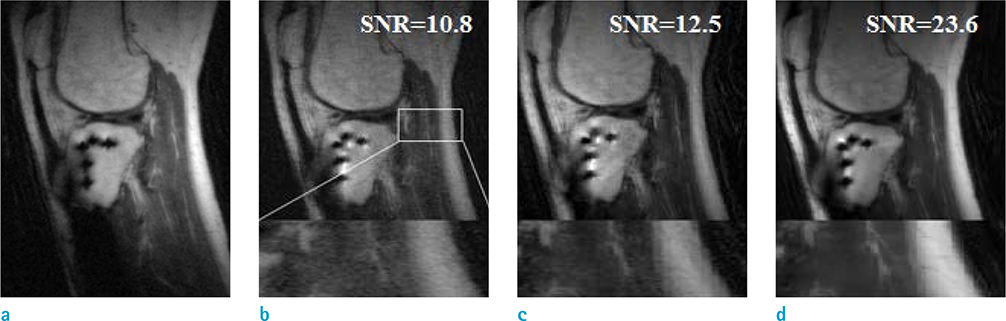
Three images reconstructed using SEMAC, SEMAC with the conventional two-step noise reduction, and the proposed image denoising for metal MRI exploiting sparsity and low rank approximation algorithm were compared. The proposed algorithm outperformed two methods and produced 119% SNR better than SEMAC and 89% SNR better than SEMAC with the conventional two-step noise reduction.
CONCLUSION
We successfully demonstrated that the proposed, novel algorithm for SEMAC, if compared with conventional de-noising methods, substantially improves SNR and reduces artifacts.

Keyword

Slice Encoding for Metal Artifact Correction; Low rank approximation; Best linear unbiased estimator; Image denoising; Sparsity

MeSH Terms

Artifacts
Least-Squares Analysis
Magnetic Resonance Imaging*
Methods
Noise
Signal-To-Noise Ratio

Figure

• 

  Fig. 1 Fully described multi-dimensional SEMAC (slice encoding for metal artifact correction) data representation.

• 

  Fig. 2 (a) Reduced data representation in the c-s dimension, (b) reduced data representation in the z-s dimension, (c) normalized singular values of (a) and (b).

• 

  Fig. 3 BLUE (best linear unbiased estimator) processing pipeline.

• 

  Fig. 4 Pre-processing of noise using low-rank approximation. 1st row (no low rank processing): (a) peripheral slice, (b) intermediate, (c) central slice, (d) peripheral slice, 2nd row (c-s low rank processing): (e) peripheral slice, (f) intermediate, (g) central slice, (h) peripheral slice, 3rd row (z-s low rank processing): (i) peripheral slice, (j) intermediate, (k) central slice, (l) peripheral slice.

• 

  Fig. 5 BLUE (best linear unbiased estimator) processing. 1st row (z-s low-rank): (a) peripheral slice, (b) intermediate, (c) central slice, (d) peripheral slice 2nd row (z-s low-rank + BLUE): (e) peripheral slice, (f) intermediate, (g) central slice, (h) peripheral slice.

• 

  Fig. 6 Sparse recovery processing: (a) z-s low-rank + BLUE, (b) z-s low-rank + BLUE + OMP, (c) magnitude different image.

• 

  Fig. 7 Comparison of knee images reconstructed using (a) TSE (turbo spin echo), (b) SEMAC (slice encoding for metal artifact correction), (c) SEMAC (slice encoding for metal artifact correction) with the conventional two-step reduction, and (d) with the proposed algorithm.

Reference

1. Cho ZH, Kim DJ, Kim YK. Total inhomogeneity correction including chemical shifts and susceptibility by view angle tilting. Med Phys. 1988; 15:7–11.

2. Koch KM, Lorbiecki JE, Hinks RS, King KF. A multispectral three-dimensional acquisition technique for imaging near metal implants. Magn Reson Med. 2009; 61:381–390.

3. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. SEMAC: Slice Encoding for Metal Artifact Correction in MRI. Magn Reson Med. 2009; 62:66–76.

4. Lu W, Pauly KB, Gold GE, Pauly JM, Hargreaves BA. Slice encoding for metal artifact correction with noise reduction. Magn Reson Med. 2011; 65:1352–1357.

5. Candes EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009; 9:717–772.

6. Cai JF, Candes EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization. 2010; 20:1956–1982.

7. Lee K, Bresler Y. ADMiRA: atomic decomposition for minimum rank approximation. IEEE Trans Inf Theory. 2010; 56:4402–4416.

8. Lee K, Bresler Y. Guaranteed minimum rank approximation from linear observations by nuclear norm minimization with ellipsoidal constraint. arXiv preprint. 2009; arXiv:0903.4742.

9. Erez Y, Schechner YY, Adam D. Space variant ultrasound frequency compounding based on noise characteristics. Ultrasound Med Biol. 2008; 34:981–1000.

10. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999; 42:952–962.

11. Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Top Magn Reson Imaging. 2004; 15:223–236.

12. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006; 52:1289–1306.

13. Daubechies I, Defrise M, De Mol D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun Pure Appl. 2004; 57:1413–1457.

14. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007; 58:1182–1195.

15. Davis G, Mallat S, Avellaneda M. Adaptive greedy approximation. Constr Approx. 1997; 13:57–98.

16. Tropp JA. Greed is good: algorithmic results for sparse approximation. IEEE Trans Inform Theory. 2004; 50:2231–2242.

17. Figueiredo MAT, Nowak RD, Wright SJ. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J Sel Top Signal Process. 2007; 1:586–597.

18. Tropp JA, Gilbert AC. Signal revocery from random measurements via orthogonal matching pursuit. IEEE Trans Inf Theory. 2007; 53:4655–4666.

19. Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med. 2008; 59:365–373.

20. Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. SIAM Review. 2001; 43:129–159.