J Korean Acad Conserv Dent.  2006 Jan;31(1):58-65. 10.5395/JKACD.2006.31.1.058.

The comparison of relative reliability on biaxial and three point flexural strength testing methods of light curing composite resin

• Seo DG
• Roh BD

• KMID: 2175786
• DOI: http://doi.org/10.5395/JKACD.2006.31.1.058

Abstract

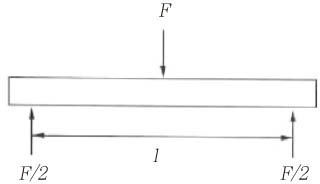
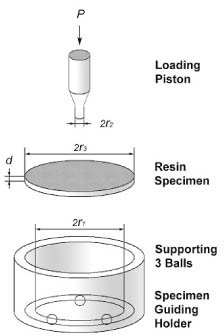
The possibility of applying a bi-axial flexure strength test on composite resin was examined using three point and bi-axial flexure strength tests to measure the strength of the light-cured resin and to compare the relative reliability using the Weibull modulus. The materials used in this study were light-curing restorative materials, MICRONEW(TM), RENEW(R) (Bisco, Schaumburg, USA). The bi-axial flexure strength measurements used the piston-on-3-ball test according to the regulations of the International Organization for Standardization (ISO) 6872 and were divided into 6 groups, where the radius of the specimens were 12 mm (radius connecting the 3-balls: 3.75 mm), 16 mm (radius connecting the 3-balls: 5 mm), and the thickness were 0.5 mm, 1 mm, 2 mm for each radius. The bi-axial flexure strength of the MICRONEW(TM) and RENEW(R) were higher than the three point flexure strength and the Weibull modulus value were also higher in all of the bi-axial flexure strength groups, indicating that the bi-axial strength test is relatively less affected by experimental error. In addition, the 2 mm thick specimens had the highest Weibull modulus values in the bi-axial flexure strength test, and the MICRONEW(TM) group showed no significant statistical difference (p > 0.05). Besides the 2 mm MICRONEW(TM) group, each group showed significant statistical differences (p < 0.05) according to the thickness of the specimen and the radius connecting the 3-balls. The results indicate that for the 2 mm group, the bi-axial flexure strength test is a more reliable testing method than the three point flexure strength test.

Keyword

Biaxial flexure strength; Three point flexure strength; Weibull modulus; Composite resin

MeSH Terms

Radius
Social Control, Formal

Figure

• 

  Figure 1 Schematic illustration of three point flexure test.

• 

  Figure 2 Schematic illustration of piston-on-three-ball bi-axial flexure test.

• 

  Figure 3 Weibull modulus graph according to specimen thickness on 3.75 mm supporting ball radius (MICRONEW™, Bisco, Schaumburg, U.S.A.).

• 

  Figure 4 Weibull modulus graph according to specimen thickness on 5 mm supporting ball radius (MICRONEW™, Bisco, Schaumburg, U.S.A.).

• 

  Figure 5 Weibull modulus graph according to specimen thickness on 3.75 mm supporting ball radius (RENEW®, Bisco, Schaumburg, U.S.A.).

• 

  Figure 6 Weibull modulus graph according to specimen thickness on 5 mm supporting ball radius (RENEW®, Bisco, Schaumburg, U.S.A.).

Reference

1. Anusavice KJ, Hojjatie B. Stress distribution in metal ceramic crowns with a facial porcelain margin. J Dent Res. 1987. 66:1493–1498.

2. Zidan O, Asmussen E, et al. Tensile strength of restorative resins. Scand J Dent Res. 1980. 88:285–289.

3. Bryant RW, Mahler DB. Modulus of elasticity in bending of composites and amalgams. J Prosthet Dent. 1986. 56:243–248.

4. Radford KC, Lange FF. Loading factors for the biaxial flexure test. J Am Ceram Soc. 1978. 61(5-6):211–213.

5. Han BS. Al2O3 selamigseu-ui yeolchunggyeog pagoe geodonggwa yeol-eunglyeog haeseog. 1997. Yeonsei Univ. Graduate School;doctorate thesis.

6. Mckinney KR, Herbert CM. Effect of surface finish on structual ceramic failure. J Am Ceram Soc. 1970. 53:513–516.

7. Kirstein AF, Woolley RM. Symmetrical bending of thin circular elastic plates of equally spaced point supports. J Res Nall Burstds. 1967. 71(C):1–10.

8. Kao R, Perrone N, Capps W. Large-deflection solution of the coaxial-ring-circular-glass-plate flexure problem. J Am Ceram Soc. 1971. 54:566–571.

9. Shetty DK, Roesinfield AR, Duckworth WH, Held PR. A Biaxial-flexure test for evaluating ceramic strength. J Am Ceram Soc. 1983. 66:36–42.

10. Marshall DB. An improved biaxial flexure test of ceramics. Am Ceram Soc Bull. 1980. 59:551–553.

11. Lamon J. Statistical approaches to failure for ceramic reliability assessment. J Am Ceram Soc. 1988. 71:106–112.

12. Wilshaw TR. Measurement of tensile strength of ceramics. J Am Ceram Soc. 1968. 51:111–117.

13. Park SE. Biaxial fracture behavior and simulation for prediction of fatigue lifetime in alumina by ball-on-3ball test. 2000. Yeonsei Univ. Graduate School;doctorate thesis.

14. Shetty DK, Roesinfield AR, Macguire P, Bansal GK, Duckworth WH. Biaxial flexure tests for ceramics. Am Ceram Soc Bull. 1980. 59(12):1193–1197.

15. Shetty DK, Roesinfield AR, Bansal GK, Duckworth WH. Biaxial fracture stuies of a glass-ceramic. J Am Ceram Soc. 1981. 64(1):1–4.

16. Williams RM, Swank LR. Use of Weibull statics to correlate MOR, Ball-on-ring, and rotational fast fracture tests. J Am Ceram Soc. 1983. 66(11):756–768.

17. Ham-Su R, Wilkinson DS. Strength of tape cast and laminated ceramics. J Am Ceram Soc. 1995. 78(6):1580–1584.

18. Chiang MYM, Tesk JA. Differences: Hertz vs finite element calculation for diametral tensile strength. J Dent Res. 1989. 68:341–348.

19. Ban S, Anusavice KJ. Influence of test method on failure stress of brittle dental materials. J Dent Res. 1990. 69(12):1791–1799.