Korean J Orthod.  2016 May;46(3):155-162. 10.4041/kjod.2016.46.3.155.

Effect of labiolingual inclination of a maxillary central incisor and surrounding alveolar bone loss on periodontal stress: A finite element analysis

• Choi SH
• Kim YH
• Lee KJ
• Hwang CJ

• KMID: 2164259
• DOI: http://doi.org/10.4041/kjod.2016.46.3.155

Abstract

OBJECTIVE
The aim of this study was to investigate whether labial tooth inclination and alveolar bone loss affect the moment per unit of force (M(t)/F) in controlled tipping and consequent stresses on the periodontal ligament (PDL).
METHODS
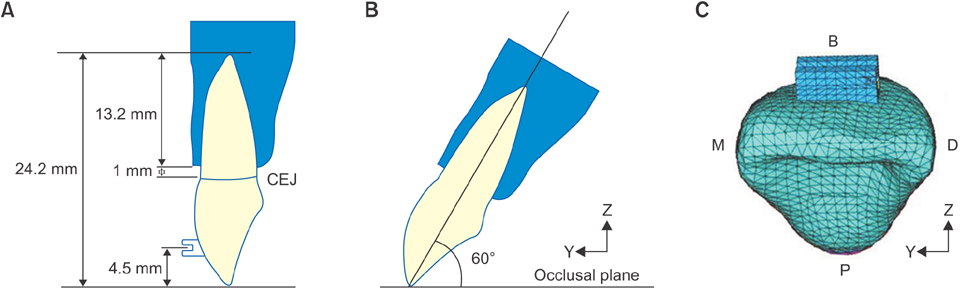
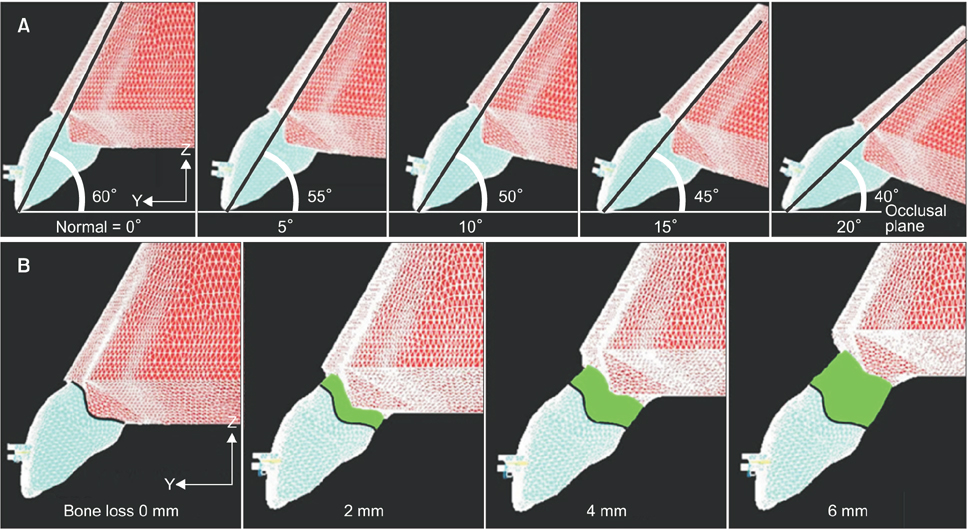
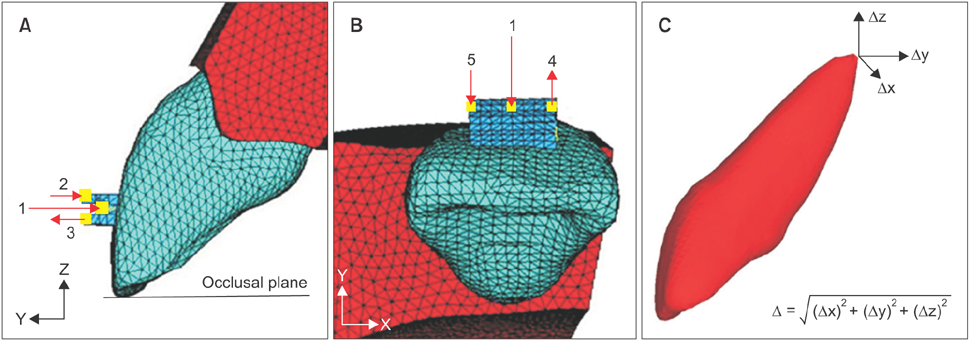
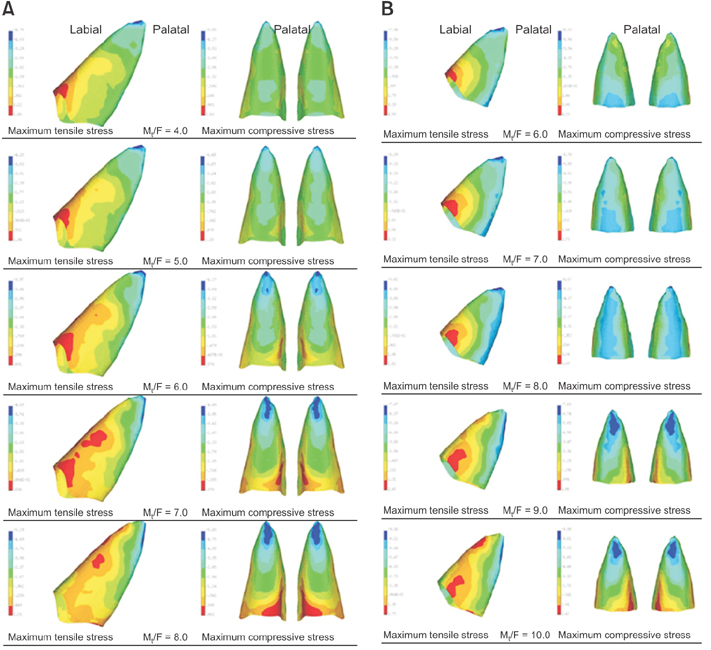
Three-dimensional models (n = 20) of maxillary central incisors were created with different labial inclinations (5°, 10°, 15°, and 20°) and different amounts of alveolar bone loss (0, 2, 4, and 6 mm). The M(t)/F necessary for controlled tipping (M(t)/F(cont)) and the principal stresses on the PDL were calculated for each model separately in a finite element analysis.
RESULTS
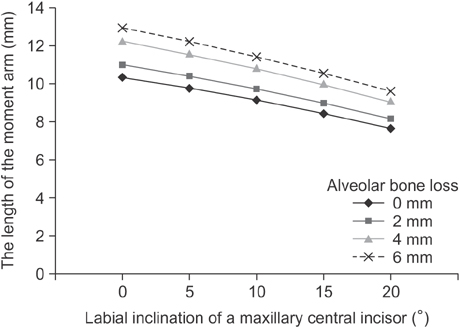
As labial inclination increased, M(t)/F(cont) and the length of the moment arm decreased. In contrast, increased alveolar bone loss caused increases in M(t)/F(cont) and the length of the moment arm. When M(t)/F was near M(t)/F(cont), increases in M(t)/F caused compressive stresses to move from a predominantly labial apical region to a palatal apical position, and tensile stresses in the labial area moved from a cervical position to a mid-root position. Although controlled tipping was applied to the incisors, increases in alveolar bone loss and labial tooth inclination caused increases in maximum compressive and tensile stresses at the root apices.
CONCLUSIONS
Increases in alveolar bone loss and labial tooth inclination caused increases in stresses that might cause root resorption at the root apex, despite the application of controlled tipping to the incisors.

Keyword

Labial tooth inclination; Alveolar bone loss; Controlled tipping; Periodontal stress

MeSH Terms

Alveolar Bone Loss*
Arm
Finite Element Analysis*
Incisor*
Periodontal Ligament
Root Resorption
Tooth

Figure

• 

  Figure 1 The basic model of an incisor. A, Tooth length, 24.2 mm; tooth root, 13.2 mm; bracket position midpoint, 4.5 mm. The alveolar bone (dark blue) is situated 1 mm above the cementoenamel junction (CEJ). B, Normal inclination of an incisor 60° from the occlusal plane. C, A tetrahedral mesh covers the tooth surface and bracket. M, Mesial; D, distal; B, buccal; P, palatal.

• 

  Figure 2 Models of incisors with different inclinations and different amounts of alveolar bone loss. A total of 20 models were created (5 different inclinations and 4 levels of bone loss). A, Experimental incisor models with labial inclinations of 5°, 10°, 15°, and 20°. B, Models demonstrating 0, 2, 4, and 6 mm of alveolar bone loss.

• 

  Figure 3 Forces associated with the 3 different loads applied to the tooth models. A, The first load (1) was a retraction force (100 gf) applied parallel to the occlusal plane at the midpoint of the bracket. The second load was a coupled force (2, 3) that created a counter-tipping moment (Mt). B, The third load was a coupled force (4, 5) that created a rotation moment (Mr). C, Calculation of the three-dimensional displacement (Δ) of the apex.

• 

  Figure 4 Changes in the length of the moment arm (the perpendicular distance between the line of action of the force and the center of resistance) according to changes in maxillary central incisor inclination and surrounding alveolar bone loss.

• 

  Figure 5 Relationship between the Mt/F ratio and principal stresses in tooth models with 20° of labial inclination. The minimum principal stress levels are indicated by triangles.

• 

  Figure 6 Incisor root stress distribution patterns under conditions with Mt/F near Mt/Fcont (red area, maximum tensile stress; blue area, maximum compressive stress). A, A tooth model with no alveolar bone loss and an incisal inclination of 15°; controlled tipping occurs at Mt/F = 6. B, A tooth model with 6 mm of alveolar bone loss and an incisal inclination of 15°; controlled tipping occurs at Mt/F = 8.

Reference

1. Gkantidis N, Christou P, Topouzelis N. The orthodontic-periodontic interrelationship in integrated treatment challenges: a systematic review. J Oral Rehabil. 2010; 37:377–390.

2. Towfighi PP, Brunsvold MA, Storey AT, Arnold RM, Willman DE, McMahan CA. Pathologic migration of anterior teeth in patients with moderate to severe periodontitis. J Periodontol. 1997; 68:967–972.

3. Cobo J, Argüelles J, Puente M, Vijande M. Dentoalveolar stress from bodily tooth movement at different levels of bone loss. Am J Orthod Dentofacial Orthop. 1996; 110:256–262.

4. Cobo J, Sicilia A, Argüelles J, Suárez D, Vijande M. Initial stress induced in periodontal tissue with diverse degrees of bone loss by an orthodontic force: tridimensional analysis by means of the finite element method. Am J Orthod Dentofacial Orthop. 1993; 104:448–454.

5. Geramy A. Alveolar bone resorption and the center of resistance modification (3-D analysis by means of the finite element method). Am J Orthod Dentofacial Orthop. 2000; 117:399–405.

6. Geramy A. Initial stress produced in the periodontal membrane by orthodontic loads in the presence of varying loss of alveolar bone: a three-dimensional finite element analysis. Eur J Orthod. 2002; 24:21–33.

7. McLaughlin RP, Bennett JC, Trevisi HJ. Systemized orthodontic treatment mechanics. Edinburgh: Mosby;2001.

8. Tian YL, Liu F, Sun HJ, Lv P, Cao YM, Yu M, et al. Alveolar bone thickness around maxillary central incisors of different inclination assessed with cone-beam computed tomography. Korean J Orthod. 2015; 45:245–252.

9. Burstone CJ. The mechanics of the segmented arch techniques. Angle Orthod. 1966; 36:99–120.

10. Cattaneo PM, Dalstra M, Melsen B. Moment-to-force ratio, center of rotation, and force level: a finite element study predicting their interdependency for simulated orthodontic loading regimens. Am J Orthod Dentofacial Orthop. 2008; 133:681–689.

11. Brezniak N, Wasserstein A. Orthodontically induced inflammatory root resorption. Part II: The clinical aspects. Angle Orthod. 2002; 72:180–184.

12. Brezniak N, Wasserstein A. Orthodontically induced inflammatory root resorption. Part I: The basic science aspects. Angle Orthod. 2002; 72:175–179.

13. Viecilli R, Katona T, Roberts W. Optimization of microCT data processing for modelling of dental structures in orthodontic studies. Comput Methods Biomech Biomed Engin. 2007; 10:257–263.

14. Viecilli RF, Katona TR, Chen J, Hartsfield JK Jr, Roberts WE. Three-dimensional mechanical environment of orthodontic tooth movement and root resorption. Am J Orthod Dentofacial Orthop. 2008; 133:791.e11–791.e26.

15. Cheng LL, Türk T, Elekdağ-Türk S, Jones AS, Petocz P, Darendeliler MA. Physical properties of root cementum: Part 13. Repair of root resorption 4 and 8 weeks after the application of continuous light and heavy forces for 4 weeks: a microcomputed-tomography study. Am J Orthod Dentofacial Orthop. 2009; 136:320.e1–320.e10. discussion 320-1.

16. Richardson ER. Comparative thickness of the human periodontal membrane of functioning versus non-functioning teeth. J Oral Med. 1967; 22:120–126.

17. Coolidge ED. The thickness of human periodontal membrane. J Am Dent Assoc. 1937; 24:1260–1270.

18. Mo SS, Kim SH, Sung SJ, Chung KR, Chun YS, Kook YA, et al. Torque control during lingual anterior retraction without posterior appliances. Korean J Orthod. 2013; 43:3–14.

19. Sung EH, Kim SJ, Chun YS, Park YC, Yu HS, Lee KJ. Distalization pattern of whole maxillary dentition according to force application points. Korean J Orthod. 2015; 45:20–28.

20. Kanjanaouthai A, Mahatumarat K, Techalertpaisarn P, Versluis A. Effect of the inclination of a maxillary central incisor on periodontal stress: finite element analysis. Angle Orthod. 2012; 82:812–819.

21. Tanne K, Sakuda M, Burstone CJ. Three-dimensional finite element analysis for stress in the periodontal tissue by orthodontic forces. Am J Orthod Dentofacial Orthop. 1987; 92:499–505.

22. Shaw AM, Sameshima GT, Vu HV. Mechanical stress generated by orthodontic forces on apical root cementum: a finite element model. Orthod Craniofac Res. 2004; 7:98–107.

23. Brunsvold MA. Pathologic tooth migration. J Periodontol. 2005; 76:859–866.

24. Sameshima GT, Sinclair PM. Predicting and preventing root resorption: Part I. Diagnostic factors. Am J Orthod Dentofacial Orthop. 2001; 119:505–510.

25. Melsen B. Adult orthodontics. Chichester, West Sussex: Blackwell Publishing;2012. p. 212.

26. Siatkowski RE. Optimal orthodontic space closure in adult patients. Dent Clin North Am. 1996; 40:837–873.

27. Tanne K, Nagataki T, Inoue Y, Sakuda M, Burstone CJ. Patterns of initial tooth displacements associated with various root lengths and alveolar bone heights. Am J Orthod Dentofacial Orthop. 1991; 100:66–71.

28. Sung SJ, Kim IT, Kook YA, Chun YS, Kim SH, Mo SS. Finite-element analysis of the shift in center of resistance of the maxillary dentition in relation to alveolar bone loss. Korean J Orthod. 2009; 39:278–288.

29. Parker RJ, Harris EF. Directions of orthodontic tooth movements associated with external apical root resorption of the maxillary central incisor. Am J Orthod Dentofacial Orthop. 1998; 114:677–683.

30. Dermaut LR, De Munck A. Apical root resorption of upper incisors caused by intrusive tooth movement: a radiographic study. Am J Orthod Dentofacial Orthop. 1986; 90:321–326.