Korean Circ J.  2011 Aug;41(8):423-430. 10.4070/kcj.2011.41.8.423.

Computational Fluid Dynamics in Cardiovascular Disease

• Lee BK

• KMID: 1826347
• DOI: http://doi.org/10.4070/kcj.2011.41.8.423

Abstract

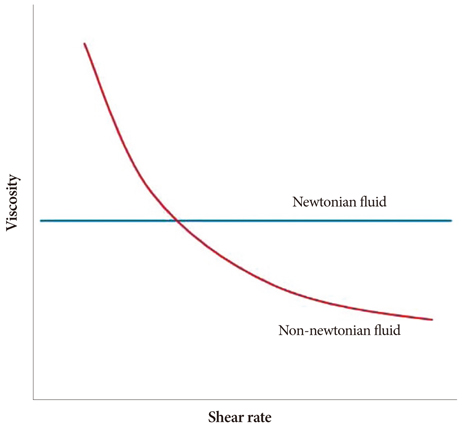
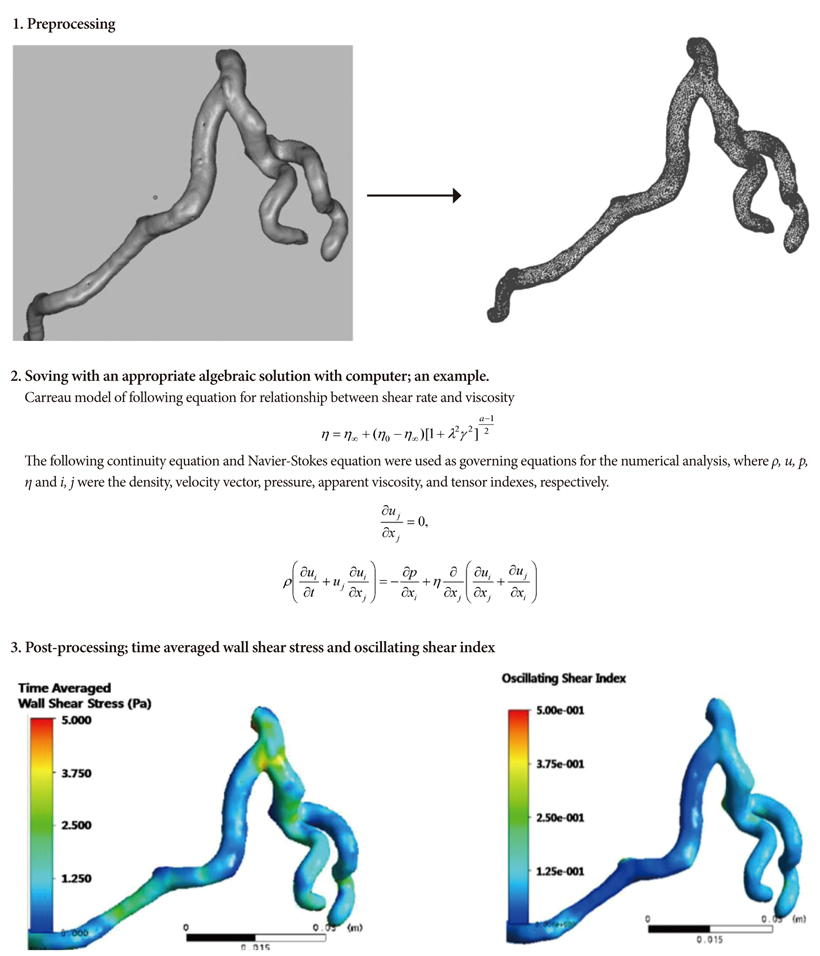
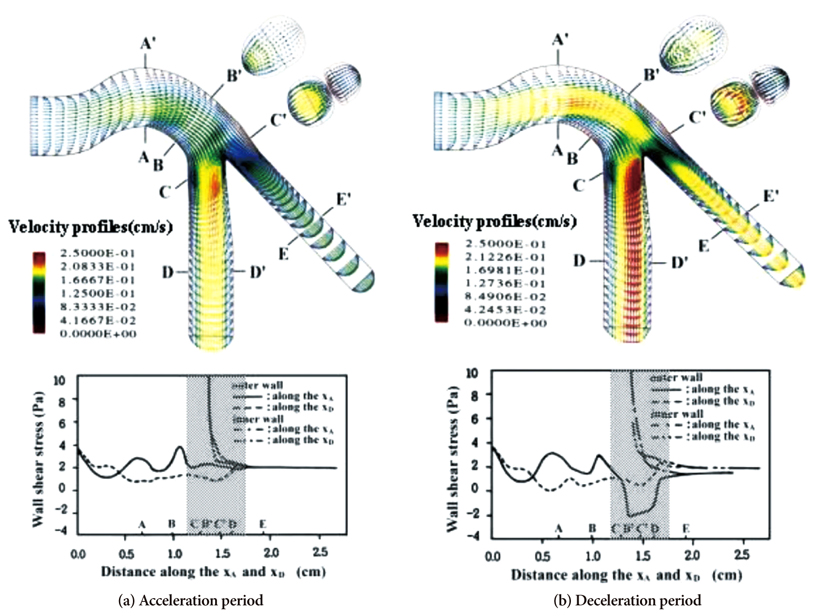
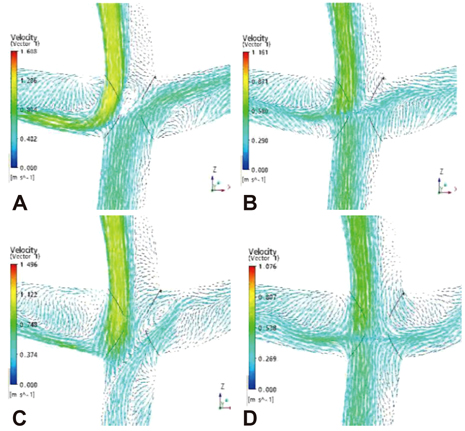
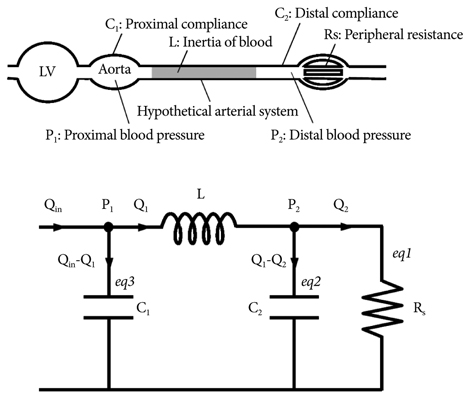
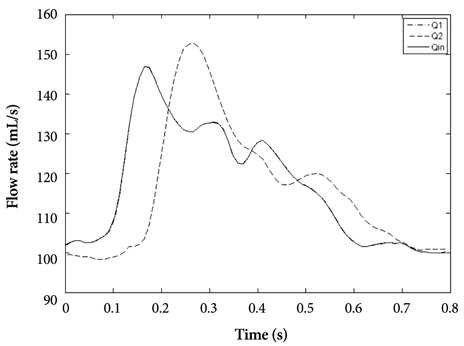
Computational fluid dynamics (CFD) is a mechanical engineering field for analyzing fluid flow, heat transfer, and associated phenomena, using computer-based simulation. CFD is a widely adopted methodology for solving complex problems in many modern engineering fields. The merit of CFD is developing new and improved devices and system designs, and optimization is conducted on existing equipment through computational simulations, resulting in enhanced efficiency and lower operating costs. However, in the biomedical field, CFD is still emerging. The main reason why CFD in the biomedical field has lagged behind is the tremendous complexity of human body fluid behavior. Recently, CFD biomedical research is more accessible, because high performance hardware and software are easily available with advances in computer science. All CFD processes contain three main components to provide useful information, such as pre-processing, solving mathematical equations, and post-processing. Initial accurate geometric modeling and boundary conditions are essential to achieve adequate results. Medical imaging, such as ultrasound imaging, computed tomography, and magnetic resonance imaging can be used for modeling, and Doppler ultrasound, pressure wire, and non-invasive pressure measurements are used for flow velocity and pressure as a boundary condition. Many simulations and clinical results have been used to study congenital heart disease, heart failure, ventricle function, aortic disease, and carotid and intra-cranial cerebrovascular diseases. With decreasing hardware costs and rapid computing times, researchers and medical scientists may increasingly use this reliable CFD tool to deliver accurate results. A realistic, multidisciplinary approach is essential to accomplish these tasks. Indefinite collaborations between mechanical engineers and clinical and medical scientists are essential. CFD may be an important methodology to understand the pathophysiology of the development and progression of disease and for establishing and creating treatment modalities in the cardiovascular field.

Keyword

Hydrodynamics; Viscosity; Cardiovascular diseases

MeSH Terms

Aortic Diseases
Cardiovascular Diseases
Cooperative Behavior
Diagnostic Imaging
Heart Diseases
Heart Failure
Hot Temperature
Human Body
Hydrodynamics
Magnetic Resonance Imaging
Viscosity

Figure

• 

  Fig. 1 Viscosity of Newtonian and non-Newtonian fluids according to shear rate.

• 

  Fig. 2 Pressure and velocity of the coronary artery and aorta as a boundary condition in the bifurcation model (Lee et al.). A: left coronary artery. B: abdominal aorta.

• 

  Fig. 3 An example of CFD in left coronary artery. Finite volume method, adapting Rhie-Chow algorithm, computed with ANSYS CFX package program (Anflux, Seoul, Korea) in SUN SPARC station 20 (Sun Korea Co., Seoul, Korea) were used. At first, a mesh or grid of region of interest is generated from the coronary extract images of computerized tomogram. All the digitalized data velocity, pressure information according as cardiac cycle as a boundary condition was selected to put into an appropriate algebraic solution. And, the next step is mathematic solving process by the computer. At this process, mechanical engineers and medical scientists should discuss about all the clinical situations for selecting an appropriate algebraic solution. Final step is visualization process for user. There are so many representative processing results, such as pressure profiles, velocity profiles, particle tracing, time-averaged wall shear stress (TAWSS), oscillating shear index (OSI), etc. This figure shows high TAWSS, OSI at bifurcation.

• 

  Fig. 4 The velocity vectors (upper) and distribution of wall shear stress (lower) in the coronary artery model. Prominent abrupt changes in velocity and wall shear stress at the outer wall around the branched site are noted during the deceleration period.

• 

  Fig. 5 Maximal velocity profile at inspiration (A) and expiration (B) in the supine position and inspiration (C) and expiration (D) in the standing position at an model of Fontan circulation. Tube structures represent cross-shaped reconstructed model of superior vena cava, inferior vena cava, right pulmonary artery, and left pulmonary artery at upper, lower, left and right tube.

• 

  Fig. 6 Modified Windkessel model for the human arterial system (Qin, Q1, and Q1 are defined as the flow rate exiting from the left ventricle during systole, the flow rate passing through the peripheral system, and the flow rate passing through the distal system, respectively. Similarly, p1 and p2 are the pressures measured at the proximal and distal locations, respectively. C1 and C2 are proximal and distal compliances where L corresponds to the inertia of blood.

• 

  Fig. 7 Proximal (Q1) and distal (Q2) flow rates in the left ventricle calculated with the Herschel-Bulkley equation.

Reference

1. Versteeg HK, Malalasekera W. Introduction To Computational Fluid Dynamics. The Finite Volume Method. 1995. 1st ed. New York: Longman Scientific & Technical.

2. Tu J, Yeoh GH, Liu C. Computational Fluid dynamics. A Practical Approach. 2008. 1st ed. Oxford: Elesevier.

3. Fung YC. Biomechanics. 1981. New York: Springer-Verlag.

4. Cho YI, Cho DJ. Hemorheology and microvascular disorders. Korean Circ J. 2011. 41:287–295.

5. Nichols WW, O'Rouke MF. McDonald's Blood Flow in Arteries Theoretical, Experimental and Clinical Principles. 2005. 5th ed. London: Hodder Arnold.

6. Lee BK, Kwon HM, Hong BK, et al. Hemodynamic effects on atherosclerosis-prone coronary artery: wall shear stress/rate distribution and impedance phase angle in coronary and aortic circulation. Yonsei Med J. 2001. 42:375–383.

7. Friedman MH, Deter OJ, Mar FF, Bargeron CB, Hutchins GM. Arterial geometry affects hemodynamics: a potential risk factor for atherosclerosis. Atherosclerosis. 1983. 46:225–231.

8. Fuster V, Badimon L, Badimon J, Chesebro JH. The pathogenesis of coronary artery disease and acute coronary syndromes. N Engl J Med. 1992. 326:242–250.

9. Lee BK, Kwon HM, Kim DS, et al. Computed numerical analysis of the biomechanical effects on coronary atherogenesis using human hemodynamic and dimensional variables. Yonsei Med J. 1998. 39:166–174.

10. Qiu Y, Tarbell JM. Numerical simulation of pulsatile flow in a compliant curved tube model of a coronary artery. J Biomech Eng. 2000. 122:77–85.

11. Ramaswamy SD, Vigmostad SC, Wahle A, et al. Fluid dynamic analysis in a human left anterior descending coronary artery with arterial motion. Ann Biomed Eng. 2004. 32:1628–1641.

12. Giannoglou GD, Soulis JV, Farmakis TM, Giannakoulas GA, Parcharidis GE, Louridas GE. Wall pressure gradient in normal left coronary artery tree. Med Eng Phys. 2005. 27:455–464.

13. LaDisa JF Jr, Olson LE, Douglas HA, Warltier DO, Kersten JR, Pagel PS. Alterations in regional vascular geometry produced by theoretical stent implantation influence distributions of wall shear stress: analysis of a curved coronary artery using 3D computational fluid dynamics modeling. Biomed Eng Online. 2006. 16:40.

14. Papafaklis MI, Bourantas CV, Theodorakis PE, Katsouras CS, Fotiadis DI, Michalis LK. Association of endothelial shear stress with plaque thickness in a real three-dimensional left main coronary artery bifurcation model. Int J Cardiol. 2007. 115:276–278.

15. Lee BK, Lee JY, Hong BK, et al. Hemodynamic analysis of coronary circulation in angulated coronary stenosis following stenting. Yonsei Med J. 2002. 43:590–600.

16. Ramaswamy SD, Vigmostad SC, Wahle A, et al. Comparison of left anterior descending coronary artery hemodynamics before and after angioplasty. J Biomech Eng. 2006. 128:40–48.

17. Sankaranarayanan M, Chua LP, Ghista DN, Tan YS. Computational model of blood flow in the aorto-coronary bypass graft. Biomed Eng Online. 2005. 4:14.

18. Freshwater IJ, Morsi YS, Lai T. The effect of angle on wall shear stresses in a LIMA to LAD anastomosis: numerical modelling of pulsatile flow. Proc Inst Mech Eng H. 2006. 220:743–757.

19. Fontan F, Baudet E. Surgical repair of tricuspid atresia. Thorax. 1971. 26:240–248.

20. Feldt RH, Driscoll DJ, Offord KP, et al. Protein-losing enteropathy after the Fontan operation. J Thorac Cardiovasc Surg. 1996. 112:672–680.

21. Starnes SL, Duncan BW, Kneebone JM, et al. Angiogenic proteins in the lungs of children after cavopulmonary anastomosis. J Thorac Cardiovasc Surg. 2001. 122:518–523.

22. Matthews IL, Fredriksen PM, Bjørnstad PG, Thaulow E, Gronn M. Reduced pulmonary function in children with the Fontan circulation affects their exercise capacity. Cardiol Young. 2006. 16:261–267.

23. Gewillig M. The Fontan circulation. Heart. 2005. 91:839–846.

24. Cheung YF, Penny DJ, Redington AN. Serial assessment of left ventricular diastolic function after Fontan procedure. Heart. 2000. 83:420–424.

25. Gerdes A, Kunze J, Pfister G, et al. Addition of a small curvature reduces power losses across total cavopulmonary connections. Ann Thorac Surg. 1999. 67:1760–1764.

26. Myers CD, Boyd JH, Presson RG Jr, et al. Neonatal cavopulmonary assist: pulsatile versus steady-flow pulmonary perfusion. Ann Thorac Surg. 2006. 81:257–263.

27. Hager A, Fratz S, Schwaiger M, Lange R, Hess J, Stern H. Pulmonary blood flow patterns in patients with Fontan circulation. Ann Thorac Surg. 2008. 85:186–191.

28. Bove EL, de Leval MR, Magliavacca F, Guadagni G, Dubini G. Computational fluid dynamics in the evaluation of hemodynamic performance of cavopulmonary connections after the Norwood procedure for hypoplastic left heart syndrome. J Thorac Cardiovasc Surg. 2003. 126:1040–1047.

29. de Zelicourt DA, Pekkan K, Parks J, Kanter K, Fogel M, Yoganathan AP. Flow study of an extracardiac connection with persistent left superior vena cava. J Thorac Cardiovasc Surg. 2006. 131:785–791.

30. Suh SH, Kaptan Y, Roh HW, et al. Estimation of Heart work by means of modified Windkessel model and different whole blood viscosity models. Proceedings of 7th International Conference on Computational Heat and Mass Transfer. 2011. Istanbul.

31. Westerhof N, Lankhaar JW, Westerhof BE. The arterial Windkessel. Med Biol Eng Comput. 2009. 47:131–141.

32. Yılmaz Y, Gündoğdu MY. A critical review on blood flow in large arteries: relevance to blood rheology, viscosity models and physiologic conditions. Korea-Aust Rheol J. 2008. 20:197–211.

33. Milner JS, Moore JA, Rutt BK, Steinman DA. Hemodynamics of human carotid artery bifurcations: computational studies with models reconstructed from magnetic resonance imaging of normal subjects. J Vasc Surg. 1998. 28:143–156.

34. Lee SW, Antiga L, Spence JD, Steinman DA. Geometry of the carotid bifurcation predicts its exposure to disturbed flow. Stroke. 2008. 39:2341–2347.

35. Lee SE, Lee SW, Fischer PF, Bassiouny HS, Loth F. Direct numerical simulation of transitional flow in a stenosed carotid bifurcation. J Biomech. 2008. 41:2551–2561.

36. Martin D, Zaman A, Hacker J, Mendelow D, Birchall D. Analysis of haemodynamic factors involved in carotid atherosclerosis using computational fluid dynamics. Br J Radiol. 2009. 82:S33–S38.

37. Hayase H, Tokunaga K, Nakayama T, et al. Computational fluid dynamics of carotid arteries after carotid endarterectomy or carotid artery stenting based on postoperative patient-specific computed tomography angiography and ultrasound flow data. Neurosurgery. 2011. 68:1096–1101. discussion 1101.

38. Xue YJ, Gao PY, Duan Q, et al. Preliminary study of hemodynamic distribution in patient-specific stenotic carotid bifurcation by image-based computational fluid dynamics. Acta Radiol. 2008. 49:558–565.

39. Hammer S, Jeays A, Allan PL, et al. Acquisition of 3-D arterial geometries and integration with computational fluid dynamics. Ultrasound Med Biol. 2009. 35:2069–2083.

40. LaDisa JF Jr, Bowers M, Harmann L, et al. Time-efficient patient-specific quantification of regional carotid artery fluid dynamics and spatial correlation with plaque burden. Med Phys. 2010. 37:784–792.

41. Marshall I. Computational simulations and experimental studies of 3D phase-contrast imaging of fluid flow in carotid bifurcation geometries. J Magn Reson Imaging. 2010. 31:928–934.

42. Groen HC, Simons L, van den Bouwhuijsen QJ, et al. MRI-based quantification of outflow boundary conditions for computational fluid dynamics of stenosed human carotid arteries. J Biomech. 2010. 43:2332–2338.

43. Frauenfelder T, Lotfey M, Boehm T, Wildermuth S. Computational fluid dynamics: hemodynamic changes in abdominal aortic aneurysm after stent-graft implantation. Cardiovasc Intervent Radiol. 2006. 29:613–623. Erratum in: Cardiovasc Intervent Radiol 2006;29:724.

44. O'Rourke MJ, McCullough JP. A comparison of the measured and predicted flowfield in a patient-specific model of an abdominal aortic aneurysm. Proc Inst Mech Eng H. 2008. 222:737–750.

45. Suh GY, Les AS, Tenforde AS, et al. Quantification of particle residence time in abdominal aortic aneurysms using magnetic resonance imaging and computational fluid dynamics. Ann Biomed Eng. 2011. 39:864–883.

46. Filipovic N, Ivanovic M, Krstajic D, Kojic M. Hemodynamic flow modeling through an abdominal aorta aneurysm using data mining tools. IEEE Trans Inf Technol Biomed. 2011. 15:189–194.

47. Karmonik C, Bismuth J, Davies MG, Shah DJ, Younes HK, Lumsden AB. A computational fluid dynamics study pre- and post-stent graft placement in an acute type B aortic dissection. Vasc Endovascular Surg. 2011. 45:157–164.

48. Tremmel M, Xiang J, Natarajan SK, et al. Alteration of intra-aneurysmal hemodynamics for flow diversion using enterprise and vision stents. World Neurosurg. 2010. 74:306–315.

49. Radaelli AG, Augsburger L, Cebral JR, et al. Reproducibility of haemodynamical simulations in a subject-specific stented aneurysm model: a report on the Virtual Intracranial Stenting Challenge 2007. J Biomech. 2008. 41:2069–2081.

50. Cebral JR, Mut F, Weir J, Putman C. Quantitative characterization of the hemodynamic environment in ruptured and unruptured brain aneurysms. AJNR Am J Neuroradiol. 2011. 32:145–151.

51. Sforza DM, Löhner R, Putman C, Cebral J. Hemodynamic Analysis of intracranial aneurysms with moving parent arteries: basilar tip aneurysms. Int J Numer Method Biomed Eng. 2010. 26:1219–1227.

52. Cebral JR, Mut F, Weir J, Putman CM. Association of hemodynamic characteristics and cerebral aneurysm rupture. AJNR Am J Neuroradiol. 2011. 32:264–270.